统计描述与分析基础：总体、样本与直方图

"本章介绍了数据的统计描述和分析，主要涉及数理统计的基础知识，包括总体、样本、描述性统计以及如何使用Matlab进行统计分析。通过频数表和直方图对数据进行初步整理和直观描述，并给出具体例子说明制作过程。" 在统计学中，数据的统计描述和分析是至关重要的，它旨在从大量的数据中提取关键信息，揭示数据的规律和特征。数理统计是基于概率论的实用学科，它关注的是受随机因素影响的数据。数据样本的规模可大可小，统计的目标是通过少数具有代表性的数值来概括整个样本集的特性。 首先，我们要理解基本概念：总体和样本。总体是研究对象的全集，比如所有产品或全体学生。个体是总体中的单个元素，可以用变量来表示，如产品的合格状态或学生的身高。样本是从总体中随机抽取的一部分，用于分析和推断总体的性质。样本容量（n）是样本中个体的数量。 描述性统计是统计学的重要组成部分，它包括收集、整理和分析数据，以展示数据的主要趋势、特征和数量关系。这一过程常常通过参数估计和假设检验来实现，它们是统计推断的基础。在实际工作中，我们通常会利用统计软件，如Matlab的统计工具箱，来简化和加速这些计算。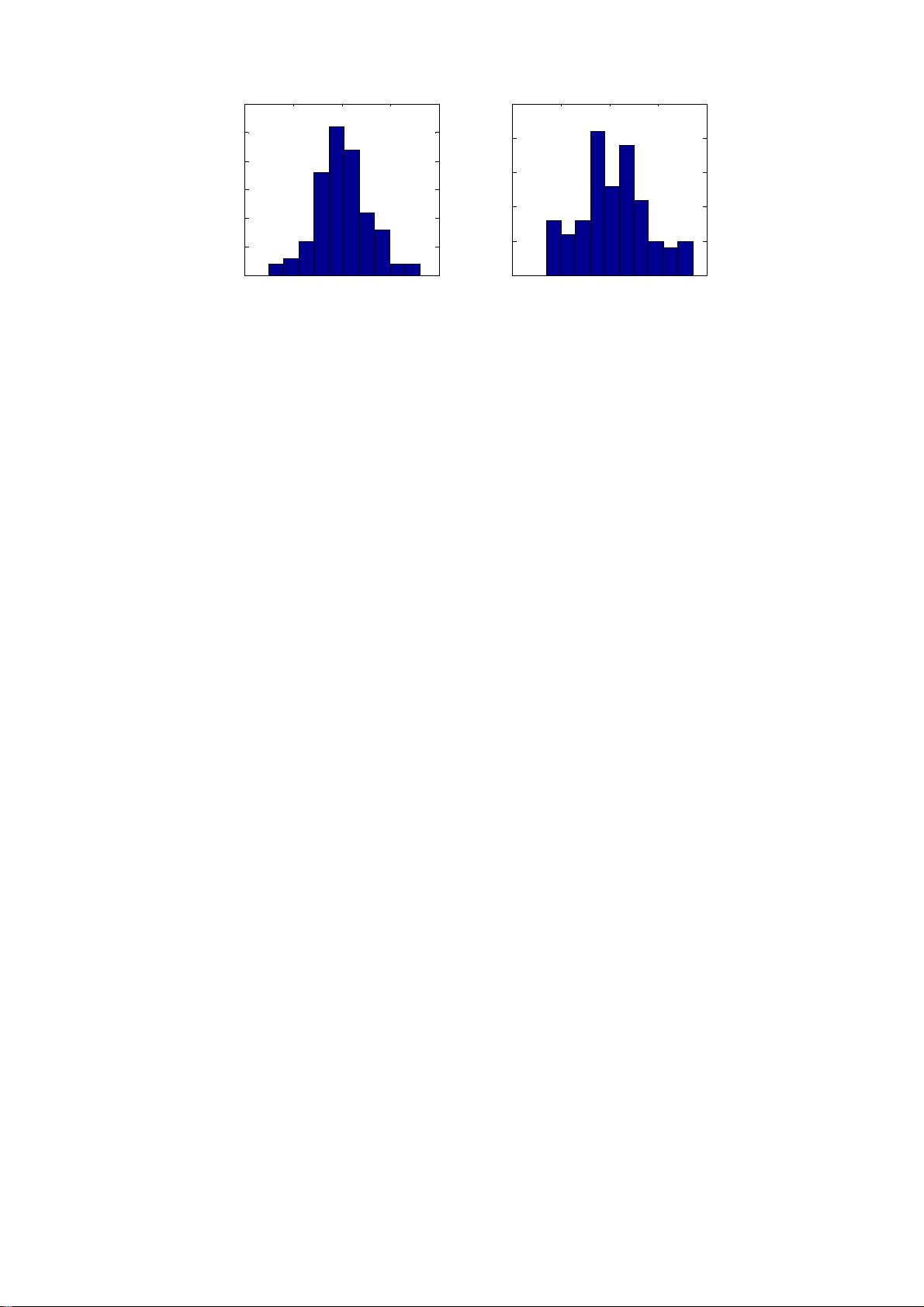 频数表和直方图是描述性统计的两种常用工具。频数表通过对数据分段并记录各段出现的次数来组织数据，而直方图则以图形形式直观地展示数据分布。对于小规模数据，我们可以手动创建这些图表；但对于大规模数据，借助软件如Matlab能更高效地完成。例如，在学校身高体重的调查中，100名学生的数据可以通过频数表和直方图来分析身高和体重的分布情况。 在Matlab中，我们可以轻松生成频数表和直方图。对于给定的身高和体重数据，我们先对数据进行分段，然后计算每个段内的频数。接着，使用直方图函数绘制图形，横坐标为数据值，纵坐标为频数。这样，我们就能清晰地看到学生身高的集中趋势和体重的分布情况，为后续的统计分析提供基础。 统计描述和分析是理解和解释数据的关键步骤，它帮助我们从复杂的数据中提取有意义的信息。通过掌握基本的统计概念，如总体、样本，以及使用有效的数据可视化工具，如频数表和直方图，我们可以更好地理解和利用数据，为决策提供支持。在实际应用中，结合概率论和强大的统计软件，如Matlab，可以进一步提高数据分析的效率和准确性。