树和二叉树的概念与基本操作

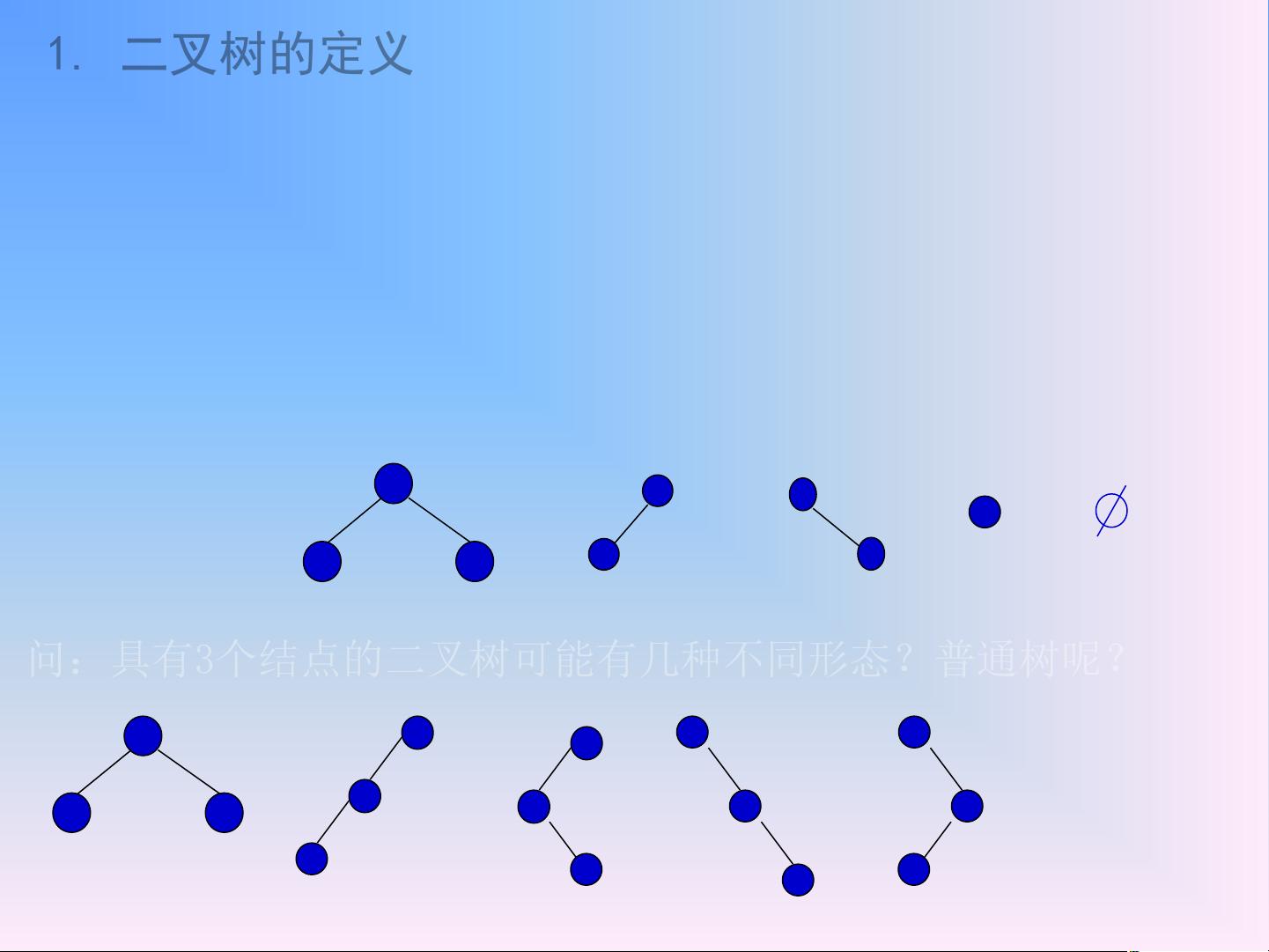
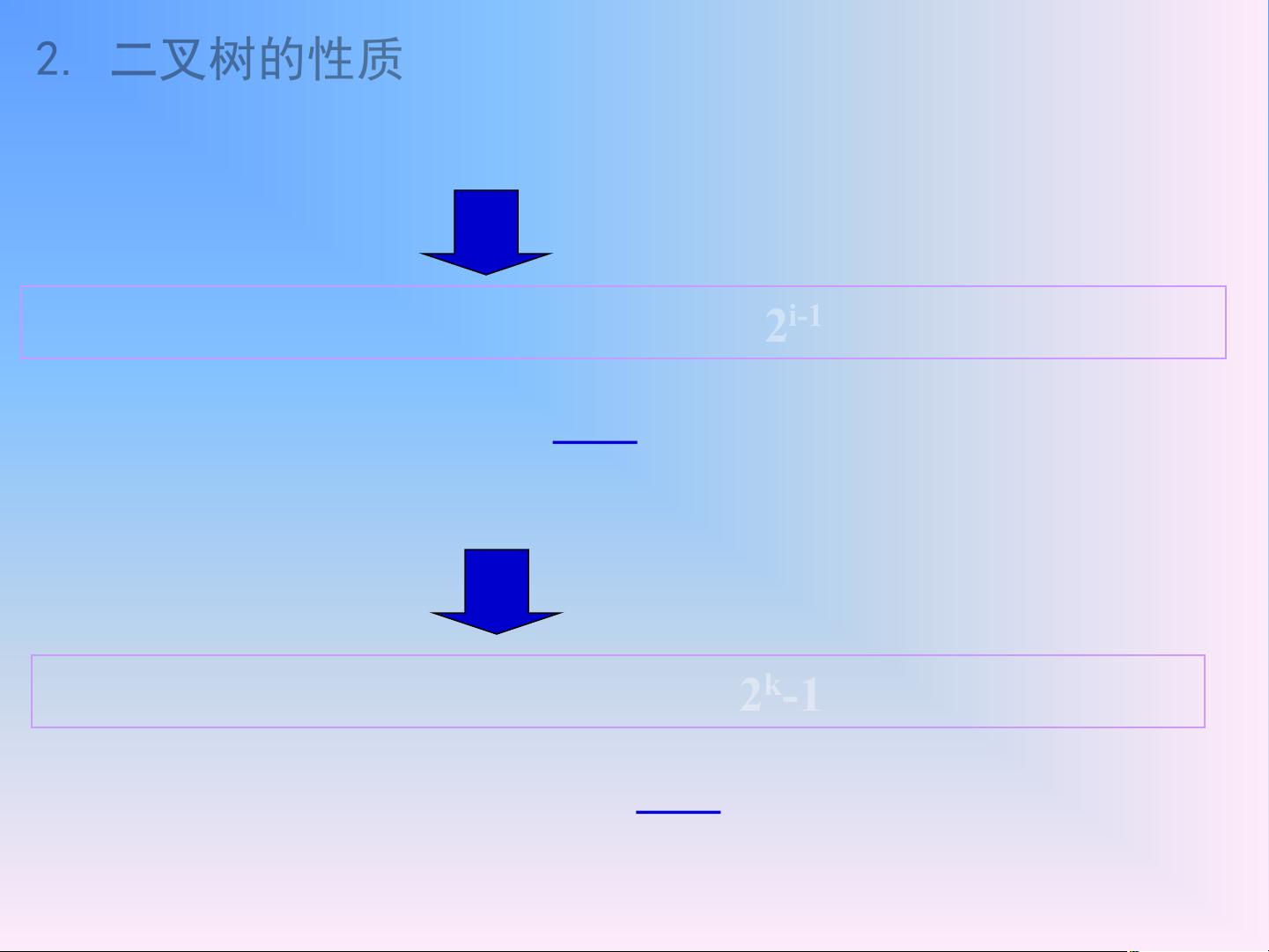
"第六章 树和二叉树" 在计算机科学中，树是一种非常重要的非线性数据结构，广泛应用于各种算法和数据组织中。本章主要涵盖了以下几个方面的知识： 1. **树的基本概念** 树是由n个(n≥0)节点组成的数据结构，其中有一个特殊的节点称为根节点，当n>1时，其余节点分为m(m≥0)个互不相交的子集合，每个子集合自身也是一棵树，称为根节点的子树。这种定义具有递归性质，因为每个子树本身也是一个树。树的表示方法有多种，如图形表示法、嵌套集合表示法、广义表表示法、目录表示法以及左孩子-右兄弟表示法。 2. **二叉树** 二叉树是特殊类型的树，其中每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树常用于搜索、排序和其他操作，如二叉搜索树和完全二叉树等。二叉树的遍历包括前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）。 3. **遍历二叉树和线索二叉树** 遍历二叉树是指按照特定顺序访问二叉树的所有节点。线索二叉树是一种为了方便进行中序遍历或其他操作而对二叉树进行的一种特殊存储结构，通过在二叉树的节点中添加线索来指示其前驱和后继节点。 4. **树和森林** 树的集合被称为森林，森林可以理解为多棵树的组合，没有公共根的树集合。在森林中，可以进行类似于树的各种操作，如转换为二叉树、森林的遍历等。 5. **赫夫曼树及其应用** 赫夫曼树（Huffman Tree）又称为最优二叉树，是一种带权路径长度最短的二叉树，常用于数据压缩。构建赫夫曼树的过程是通过赫夫曼编码，将频率高的字符编码为较短的二进制码，从而提高压缩效率。 在树的抽象数据类型（ADTTree）定义中，数据对象D代表树中的节点，数据关系R定义了节点之间的关系。基本操作P包括创建树、查找、插入、删除等。树中的术语如根、叶子、双亲、孩子、兄弟、堂兄弟、祖先和子孙等，都定义了节点之间的相对位置和关系。 树的度是节点的子树数量，即节点的直接后继数量。一个节点的度可以是0（叶子节点）、1、2或大于2。无序树中，子树的顺序没有限制，而在有序树中，如二叉树，子树的顺序是有规定的，例如在二叉搜索树中，左子树的值总是小于父节点，右子树的值总是大于父节点。 在实际编程中，理解和掌握这些概念对于实现各种树相关的算法至关重要，如二叉搜索树、AVL树、红黑树等。这些数据结构在操作系统、数据库系统、编译原理等领域都有广泛应用。