粒子群算法详解与MATLAB实现

"粒子群算法详解matlab代码" 粒子群算法(PSO，Particle Swarm Optimization)是一种基于群体智能的优化算法，灵感来源于自然界中鸟群觅食的行为。该算法由Eberhart和Kennedy在1995年首次提出，主要用于解决连续优化问题。在PSO算法中，每个解决方案被称为“粒子”，粒子在解空间中移动，通过其自身的最佳位置（个人最优，pBest）和群体的最佳位置（全局最优，gBest）来调整自己的速度和方向，以寻找最优解。 1. **粒子群算法的基本概念** - **粒子**: 粒子代表解空间中的一个潜在解，具有坐标和速度，这两个属性在算法迭代过程中动态更新。 - **速度**: 粒子的速度决定了它在解空间中移动的方向和距离，通常由当前速度和更新规则决定。 - **适应值/Fitness Value**: 衡量一个粒子解决方案的质量，通常由目标函数计算得出。 - **个人最优(pBest)**: 每个粒子在搜索过程中遇到的最优解。 - **全局最优(gBest)**: 整个粒子群中的最优解，所有粒子中适应值最好的粒子的位置。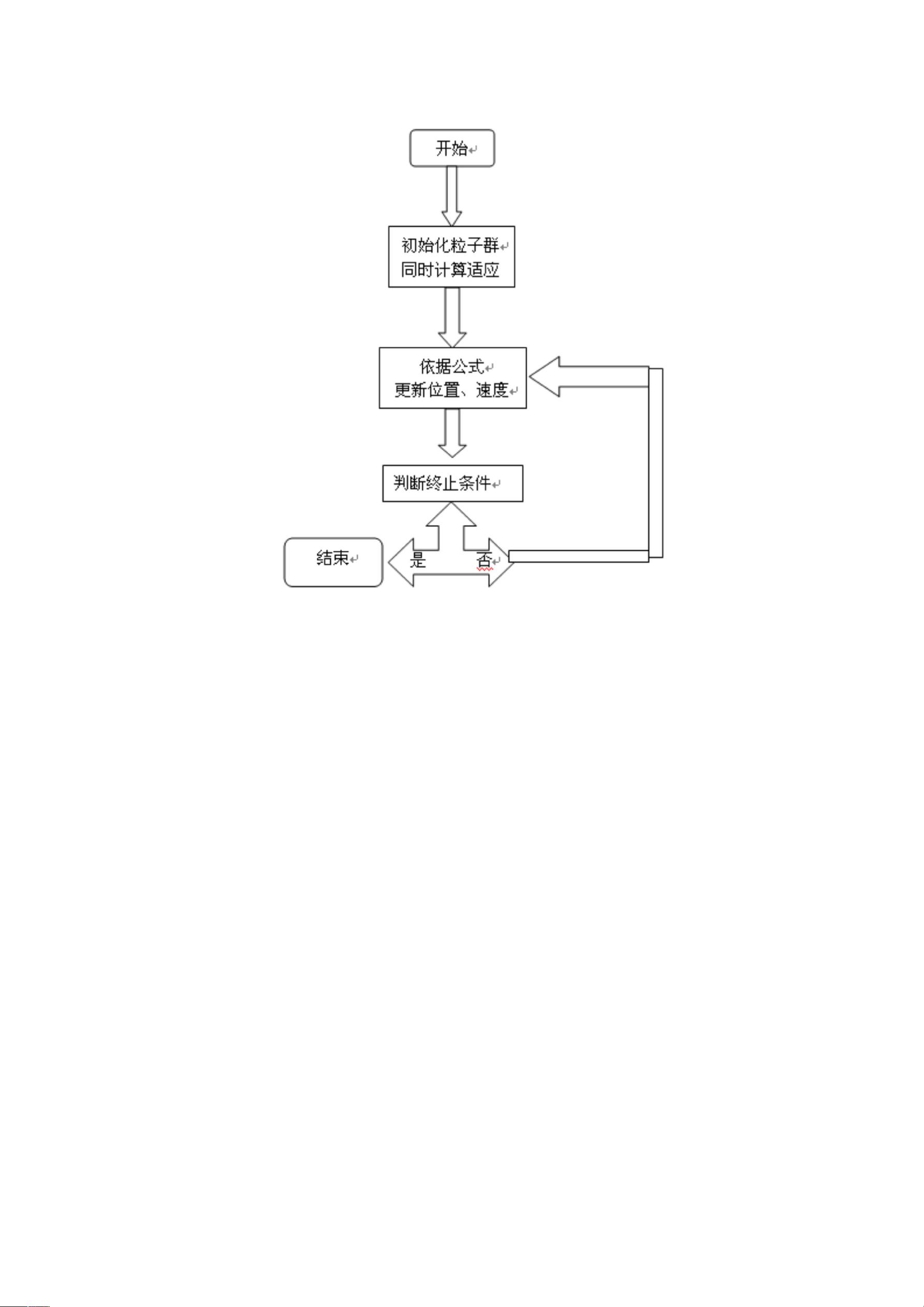 2. **粒子群算法的运作机制** - **初始化**: 随机生成一组粒子，分配初始位置和速度。 - **迭代过程**: 1. 计算每个粒子的适应值。 2. 更新每个粒子的个人最优(pBest)，如果当前粒子的适应值优于之前记录的pBest，则更新pBest。 3. 更新全局最优(gBest)，如果某个粒子的pBest优于当前的gBest，则更新gBest。 4. 更新粒子速度和位置，速度的更新公式通常包含当前速度、个人最优位置和全局最优位置的影响，以及惯性和随机因素。 5. 重复上述步骤，直到达到预设的迭代次数或满足停止条件。 3. **MATLAB实现** 在MATLAB中实现PSO算法，需要定义以下关键部分： - 初始化函数：创建粒子群并设置初始位置和速度。 - 适应度函数：计算每个粒子的适应值。 - 更新规则：设计速度和位置更新的逻辑。 - 主循环：执行迭代过程，包括计算适应值、更新pBest、gBest和速度位置。 4. **优化问题的多样性** PSO算法可以应用于各种优化问题，如函数优化、工程设计、机器学习模型参数调优等。由于其全局探索能力和简单实现，PSO在实际应用中受到欢迎，但也存在收敛速度慢和易陷入局部最优的缺点。 5. **改进策略** 为了克服原版PSO的问题，研究人员提出了一系列改进策略，如引入惯性权重、自适应调整速度边界、混沌注入、精英保留等，以提高算法的性能和稳定性。 6. **MATLAB代码示例** MATLAB代码通常包括定义粒子结构、初始化、适应度计算、更新规则和主循环等部分。具体代码会涉及矩阵操作、随机数生成以及自定义函数的调用，实现时需要结合具体问题进行调整。 7. **互联网应用** 在互联网行业中，PSO算法可以用于网络资源调度、路由优化、推荐系统个性化参数调整、广告投放策略优化等多个方面，体现了群体智能在解决复杂问题中的潜力。 粒子群算法是一种借鉴生物群体行为的优化工具，通过模拟鸟群觅食的行为，能够在多维度的优化问题中寻找全局最优解。在MATLAB中实现PSO，可以帮助工程师和科研人员便捷地解决各类优化问题。