数字电子技术基础：数制与码制转换解析

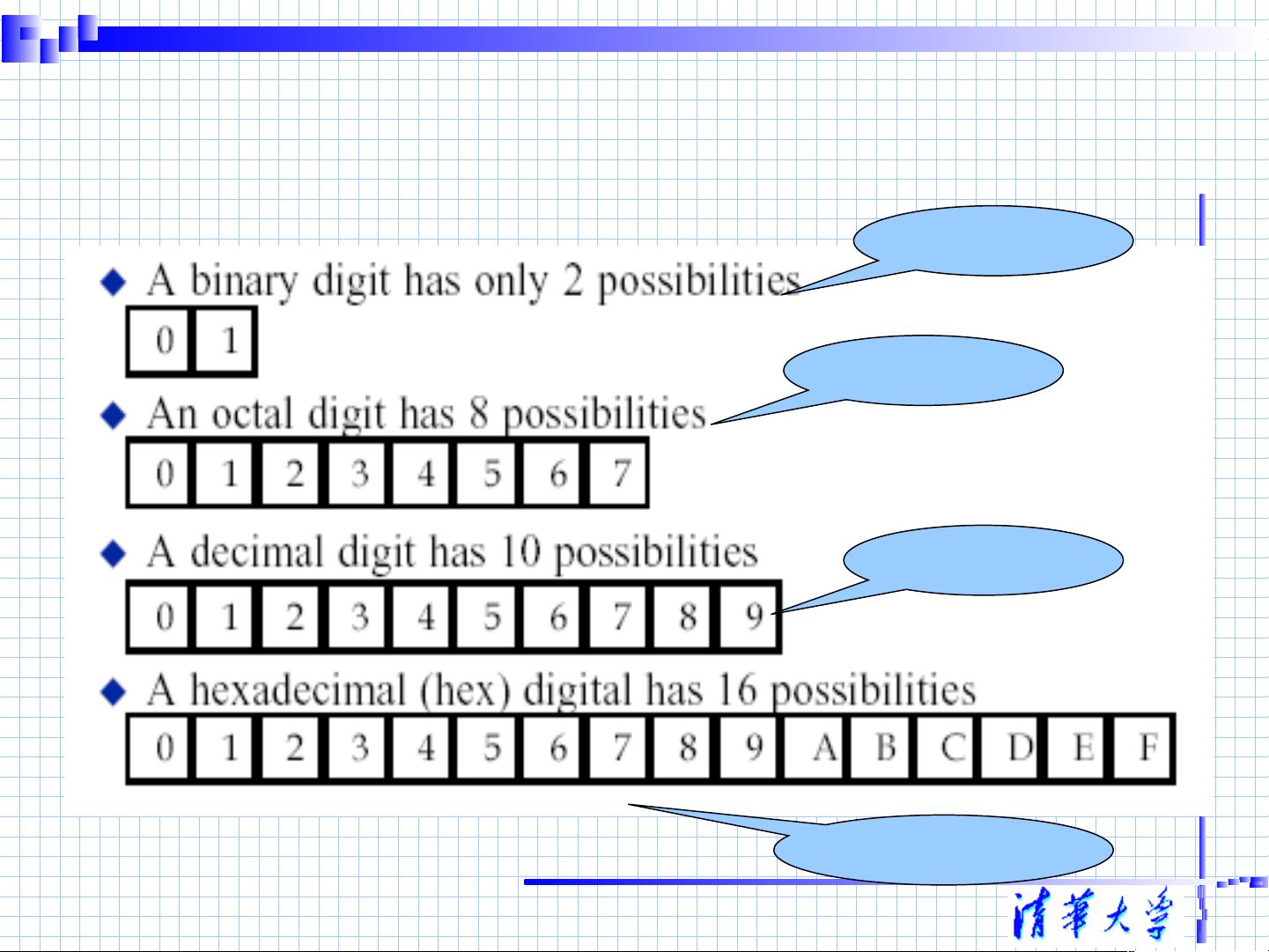
"这是一份来自广东工业大学的《数字电子技术基础》第六版的教学课件，由清华大学电子学教学组制作。课件包含了关于数制和码制的基础知识，包括各种常用的数制转换方法，以及二进制算术运算和补码运算的详细解释。" 在数字电子技术中，数制和码制是基础概念，对于理解和操作数字电路至关重要。数制是指用于表示数值大小的系统，其中每一位的构成和进位规则决定了具体的数制类型。常见的数制有十进制、二进制、八进制和十六进制。例如，二进制数制遵循“逢二进一”的规则，而八进制则是“逢八进一”，以此类推。 数制间的转换是数字电路中的常见操作。例如，可以从二进制转换为十进制，反之亦然。转换方法包括对每位的权重进行计算，然后累加得到目标数制的数值。对于小数部分，转换过程涉及到幂的计算。此外，还有二进制与十六进制之间的转换，通常通过将二进制分组并映射到相应的十六进制值来完成。 码制则是用于表示不同事物或状态的编码规则，例如，不同事物的代号可以通过特定的代码来表示。在数字电子技术中，码制的选择会影响数据的存储和传输方式。例如，二进制码可以用来表示正负数，其中最高位作为符号位，0代表正，1代表负。 二进制算术运算是数字电路中基础且重要的部分。由于二进制的“逢二进一”特性，加减乘除都可以通过移位和相加操作来实现，这简化了硬件设计，使得二进制运算在数字系统中广泛使用。二进制运算还包括对正负数的处理，其中补码是一种关键的概念。正数的补码与其原码相同，而负数的补码是其数值位逐位取反后加1。补码运算使得减法可以通过加补码来实现，例如10-5等同于10+(-5的补码)，这样简化了电路设计。 在补码运算中，当两个负数相加或者一个负数和一个正数相加时，可能需要考虑进位和溢出的问题。例如，1011（-3）加上1001（-7）的结果是0100（4），这表明在模12的环境下，-3和-7相加等于4。类似地，如果两个补码表示的二进制数相加，符号位的处理可以帮助我们确定结果的符号。 这份教学课件提供了关于数制转换、二进制算术运算和补码表示的深入理解，对于学习数字电子技术的学生来说是非常宝贵的资源。通过学习这些基础知识，学生可以更好地掌握数字电路的工作原理，并为进一步学习数字逻辑、微处理器和数字系统设计打下坚实的基础。