MATLAB实现信号频域分析技巧

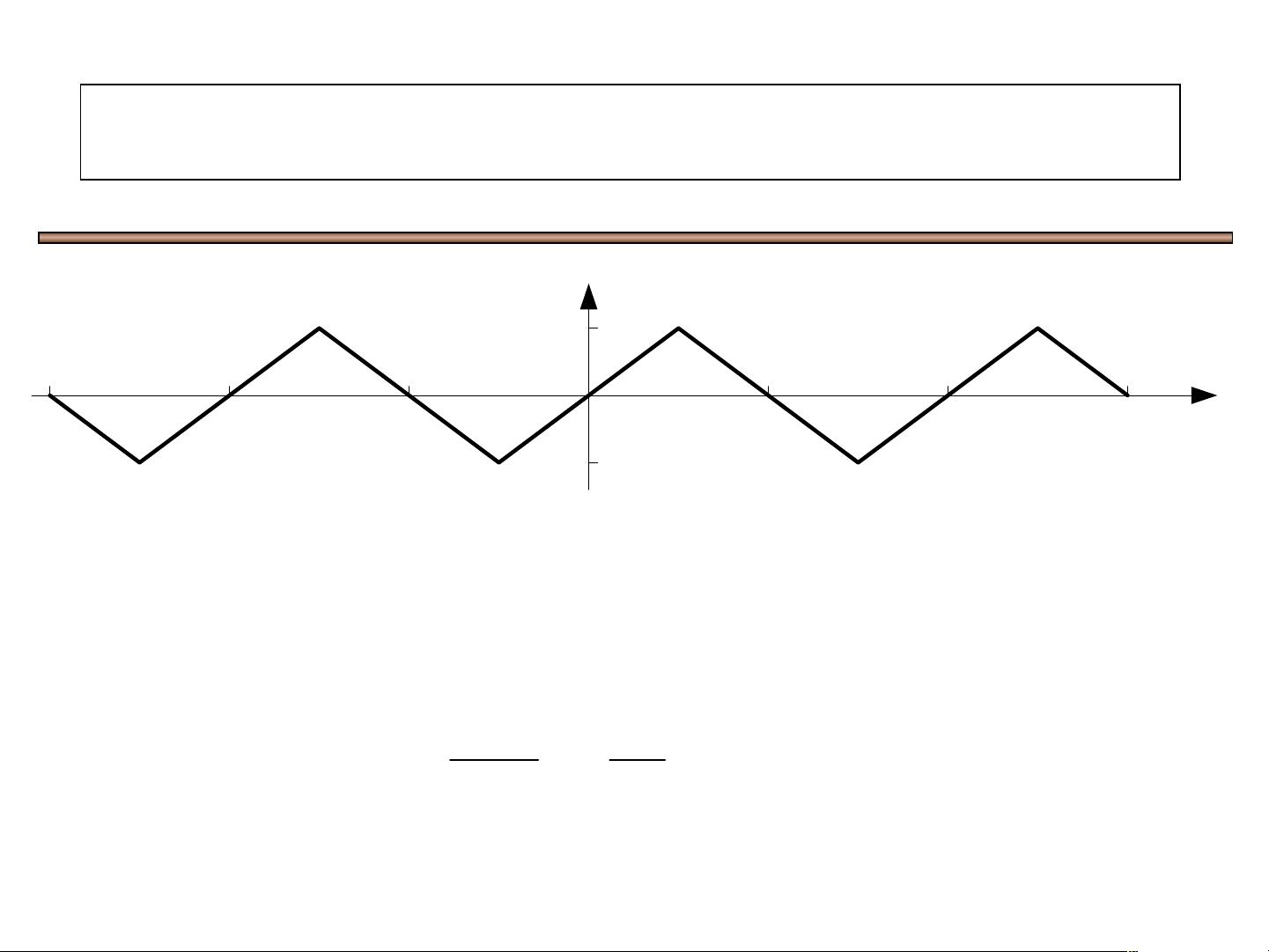
"利用MATLAB进行信号的频域分析.ppt" 在MATLAB中进行信号的频域分析是理解和处理各种类型信号的重要手段。频域分析可以帮助我们揭示信号在不同频率成分上的分布情况，这对于通信、音频处理、图像处理、控制系统等领域都具有重要意义。本资源主要介绍了如何利用MATLAB来实现周期信号和非周期信号的频域分析。 1. 周期信号频谱的MATLAB实现： 在MATLAB中，周期信号的频谱通常通过傅里叶级数或快速傅里叶变换(FFT)来计算。傅里叶级数用于将周期性信号分解为一系列正弦和余弦函数的线性组合。例如，对于一个周期三角波信号，可以使用傅里叶级数的系数Cn来表示，其中Cn可以通过离散傅里叶变换得到。在MATLAB中，`abs(Cn)`函数用于获取幅度特性，而`angle(Cn)`函数用于获取相位特性。为了可视化这些特性，可以使用`stem`函数绘制频谱图。 示例代码： ```matlab N = 8; % 周期数 n1 = -N:-1; % 计算n=-N到-1的Fourier系数 c1 = -4*j*sin(n1*pi/2)/pi^2./n1.^2; % 计算负半周系数 c0 = 0; % 计算n=0时的Fourier系数 n2 = 1:N; % 计算n=1到N的Fourier系数 c2 = -4*j*sin(n2*pi/2)/pi^2./n2.^2; % 计算正半周系数 cn = [c1 c0 c2]; % 合并系数 n = -N:N; % 频率轴 subplot(2,1,1); stem(n, abs(cn)); ylabel('Cn的幅度'); subplot(2,1,2); stem(n, angle(cn)); ylabel('Cn的相位'); xlabel('\omega/\omega0'); ``` 2. 数值积分分析非周期信号频谱： 对于非周期信号，不能直接应用傅里叶级数，但可以通过数值积分方法来估计其频谱。例如，可以使用MATLAB的`integral`函数对信号进行积分，然后通过逆傅里叶变换得到频谱。这通常用于分析瞬态信号或非周期性事件。 3. 周期矩形脉冲的Fourier级数： 周期矩形脉冲的傅里叶级数表示式涉及到无穷级数的求和，其中系数Cn可以计算得到。在MATLAB中，可以编写程序来求解这些系数，并根据级数展开的前N项来近似重构信号。 示例： ```matlab A = 1; T = 2; f0 = 1; % 参数设置 Cn = A * (1 - (-1)^n) / (1 - (2 * n * pi / f0)^2); % Fourier系数计算 t = -T:T:0.01; % 时间轴 x_approx = sum(Cn .* cos(2 * pi * f0 * n * t)); % 信号近似 plot(t, x_approx); % 绘制近似波形 ``` 4. Gibbs现象： 在使用有限项的傅里叶级数近似周期信号时，可能会观察到Gibbs现象，即在信号的突变点附近出现振荡。这是由于无限级数被截断导致的，通常可以通过增加级数项数来减小这种现象。 总结来说，MATLAB提供了强大的工具集来进行信号的频域分析，包括傅里叶变换、数值积分和信号重构等方法，这在实际工程和科研中有着广泛的应用。通过学习和掌握这些工具，我们可以更深入地理解信号的本质和特性。