Tarjan算法详解与实现

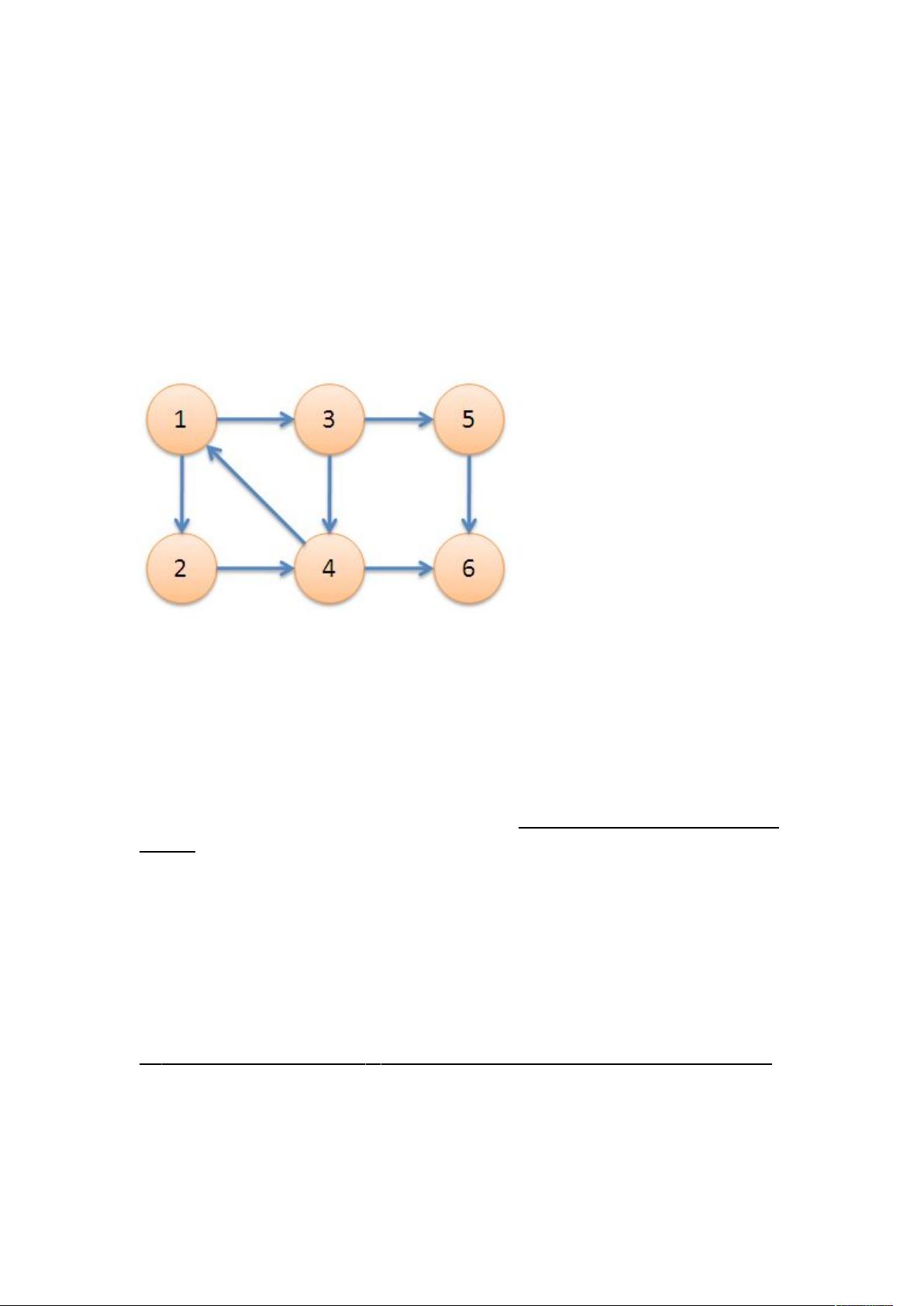
"Tarjan算法用于求解有向图的强连通分量，由著名计算机科学家Robert Tarjan发明。此算法基于深度优先搜索，能以O(N+M)的时间复杂度找到强连通分量，优于O(N^2+M)的传统方法。" 在有向图中，强连通分量是指图中任意两个顶点之间都存在双向路径的子图。如果整个图中任何两个顶点都强连通，则称图是强连通图。对于非强连通的有向图，其最大的强连通子图即为强连通分量。例如，在一个有向图中，如果子图{1,2,3,4}中的任意两个顶点都可以通过边互相到达，那么这个子图就是一个强连通分量。 Tarjan算法的核心在于深度优先搜索（DFS）和堆栈操作。算法的主要步骤如下： 1. 初始化：为每个节点分配DFN（深度优先次序编号）和Low值，均设置为递增的索引值，同时将起始节点压入堆栈。 2. 遍历边：对于图中的每一条边(u, v)，如果节点v未被访问过，则调用tarjan(v)进行递归搜索；如果v已经在堆栈中，表示u和v之间存在后向边，此时更新Low[u]为Low[u]和DFN[v]的较小值。 3. 强连通分量检测：当DFN[u]等于Low[u]时，说明以u为根的搜索子树形成一个强连通分量。此时，从栈顶开始弹出节点，直到找到u，弹出的节点序列即为一个强连通分量。 算法的伪代码如下： ``` tarjan(u): DFN[u] = Low[u] = ++Index // 为节点u设定次序编号和Low初值 Stack.push(u) // 将节点u压入栈中 foreach (u, v) in E // 枚举每一条边 if (vis_not_visted(v)) // 如果节点v未被访问过 tarjan(v) Low[u] = min(Low[u], Low[v]) elseif (v in S) // 如果节点v在栈内 Low[u] = min(Low[u], DFN[v]) if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根 repeat v = S.pop // 弹出栈顶节点v print v // 打印属于该强连通分量的节点 until (u == v) ``` 在实际运行过程中，算法会从某个起点开始进行DFS，例如从节点1开始，将遍历到的节点依次加入堆栈。当遇到节点u=6时，算法会继续深入搜索，直至找到所有与6强连通的节点，并将它们作为一个强连通分量处理。 Tarjan算法不仅用于求解强连通分量，还有其他应用，如求解有向图的双连通分量和离线最近公共祖先问题。其高效性在于利用了DFS的性质和堆栈来实时检测强连通分量，避免了不必要的回溯和重复计算。