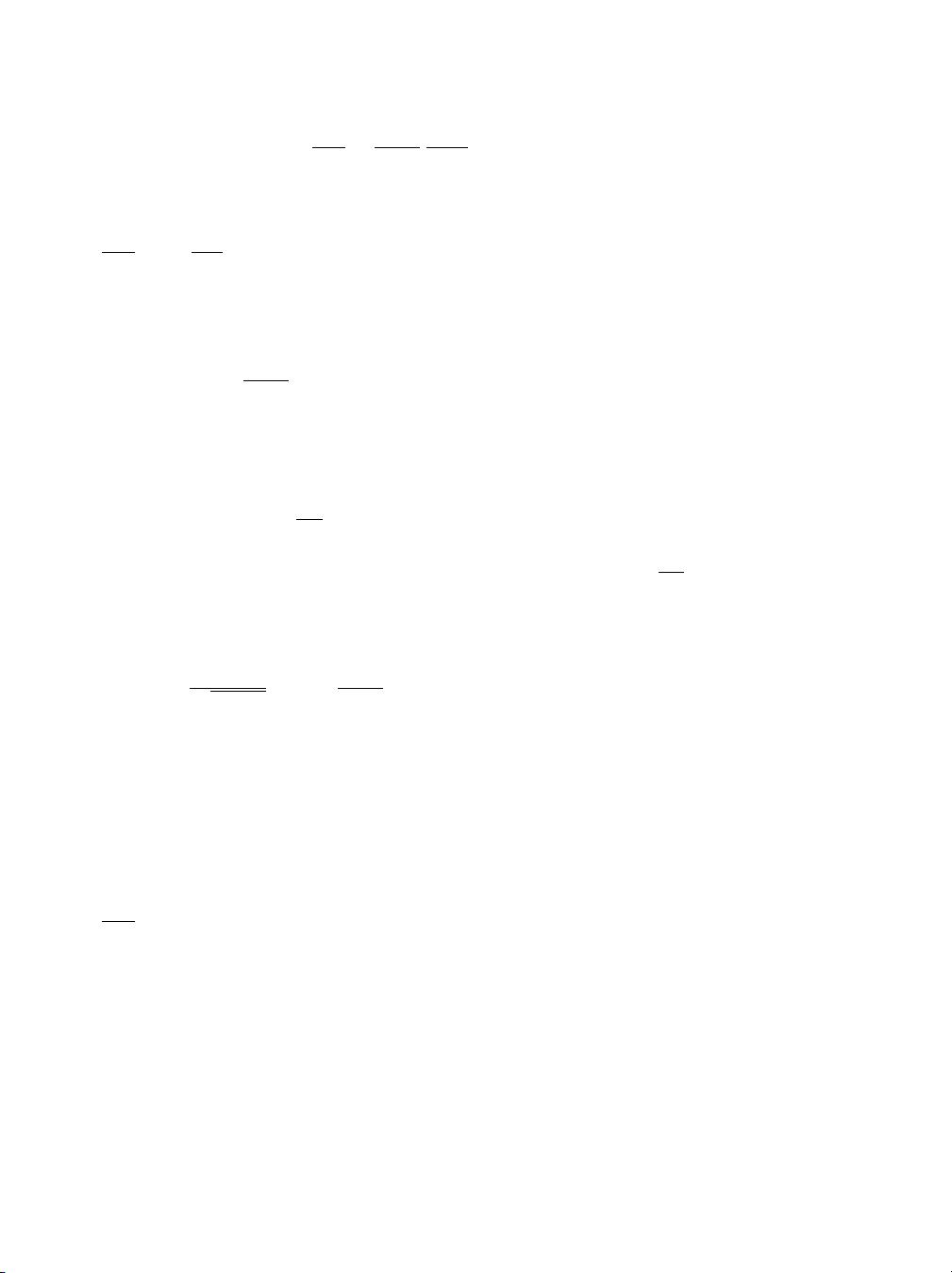异常扩散的分数动力学视角：随机游走指南
需积分: 12 29 浏览量
更新于2024-07-22
收藏 1.31MB PDF 举报
"这篇文章是Ralf Metzler和Joseph Klafter合著的《The Random Walk's Guide to Anomalous Diffusion: A Fractional Dynamics Approach》，发表在2000年的Physics Reports上。该文深入探讨了异常扩散现象，特别关注了随机游走理论在复杂系统中的应用，提供了一个基于分数动力学的方法。"
文章首先介绍了为什么我们要关注异常扩散以及分数方程的重要性。异常扩散是指物质或能量在空间中的扩散速度与常规扩散不同，它在很多自然和工程系统中都有所体现，如生物体内的分子运输、金融市场中的价格波动以及多孔介质中的流体传播等。相对于传统的布朗运动，异常扩散表现出更广泛的动态行为。
接着，作者回顾了异常动力学在复杂系统中的历史背景，指出这一领域的发展源于对非线性、非局部效应和记忆效应的研究。这些效应在经典随机游走模型中难以体现，但却是许多真实世界过程的关键特征。
在文章的主体部分，作者从连续时间随机游走理论出发，引入分数阶微分方程来描述异常扩散。这种分数动力学方法能够捕捉到亚线性和超线性的扩散行为，即扩散系数随时间呈幂律增长或减小。分数阶微分方程能够更好地模拟系统的长期依赖性和非局部性质，这在常规的局部差分模型中是无法实现的。
他们详细讨论了各种分数阶随机过程，如分数布朗运动、分数维和分数阶Cattaneo方程等，并阐述了它们在模拟实验观测中的应用。此外，文章还涵盖了用于分析和解释实验数据的统计工具，如幂律尾部分布和自相似性。
在理论模型和实验观测的比较中，作者强调了分数动力学模型的适用性和预测能力，它们能够更好地拟合和解释那些不符合经典随机游走理论的数据。同时，他们也讨论了这些模型在物理、化学、生物学和工程领域的应用实例。
这篇文章为理解异常扩散提供了一个全面而深入的视角，通过分数动力学方法揭示了随机游走行为的复杂性和多样性，对于从事相关研究的科学家来说是一份宝贵的参考资料。
di!usion equations for transport on fractal structures were shown to comply with the basic
properties, like the propagator (8), the returning probability to the origin, the mean squared
displacement, and the non-Markovian nature [183,184,225].
For homogeneous, isotropic systems which we are interested in, one knows from random walk
models that the propagator behaves asymptotically like
=(r, t)&b
t\ABm@exp(!b
mJ) (9)
with m"dr/t?, l"1/(1!a/2), b"!d(1!a)/(2!a), and b
and b
are constants depending
on a and the dimension d [238,239]. Such behaviour is reproduced by the fractional di!usion
equations that were anticipated by Balakrishnan [173] and "rst formulated by Wyss [174], and
Schneider and Wyss [175]. In Section 3 we show that the asymptotic behaviour (9) is consistent
with the asymptotic expansion of the exact solution of the fractional di!usion equation. Fractional
kinetic equations, their foundation and solution form the centre-piece of this report.
In what follows, we present the basic principles and physical properties connected with fractional
kinetic equations. We show that fractional equations arise naturally in the di!usion limit of certain
random walk schemes. By discussing methods of solution and deriving explicit solutions, we
demonstrate the usefulness of the fractional approach. At "rst, we introduce FDEs basing on the
continuous time random walk model where the transport events are subject to broad statistics.
Subsequently, FDAEs and FFPEs are presented and they describe the transport in an external
velocity or force "eld. In the "nal section, a physical derivation on the basis of a Langevin equation
with white Gaussian noise is discussed which leads to a fractional Klein}Kramers equation. From
the latter, the FFPE is consistently recovered. In the Appendices we have compiled some basic
de"nitions and useful relations which are of relevance in the main text. Thus, we give a primer on
fractional calculus and the special functions which emerge when dealing with fractional di!erential
equations, as well as a short introduction to LeH vy stable laws. Finally, we list the abbreviations
and the notation used. Note that throughout the text we denote the Laplace and Fourier
transforms of a function by stating the explicit dependence on the associated variable, e.g.
=(k, u)"F+L+=(x, t); tPu,; xPk,.
The numerous illustrations spread throughout the text are to visualise the often striking
di!erences in functional behaviour of the normal and anomalous cases, especially the perseverance
of the initial condition in the subdi!usive domain.
The discussion in the remainder of this report is restricted to the one-dimensional case, with special
emphasis on subdi!usion phenomena. The equations which describe subdi!usion presented in the
text can be extended to higher dimensions through a replacement of the derivatives in respect of the
position coordinate by corresponding orders of the operator. Some remarks on higher-dimensional
systems are contained in Ref. [215]. For those equations which describe situations with LeH vy
distributed jump lengths and which therefore contain a generalised Laplacian, we refer to the
de"nitions in Ref. [226] and the discussions in Refs. [156}158] for the multi-dimensional case.
3. From continuous time random walk to fractional di4usion equations
In our quest of establishing the fractional di!usion equation (FDE), we borrow from the ideas of
connecting the random walk approach with the continuum description through the di!usion
R. Metzler, J. Klafter / Physics Reports 339 (2000) 1}77 13
剩余76页未读，继续阅读
2021-05-20 上传
2015-09-22 上传
2021-05-04 上传
2021-02-07 上传
2021-02-06 上传
2021-02-07 上传
2021-02-21 上传
2021-03-21 上传
2021-04-22 上传
Pannos
- 粉丝: 0
- 资源: 3
我的内容管理
展开
