牛顿法与拟牛顿法：优化利器与复杂度应对

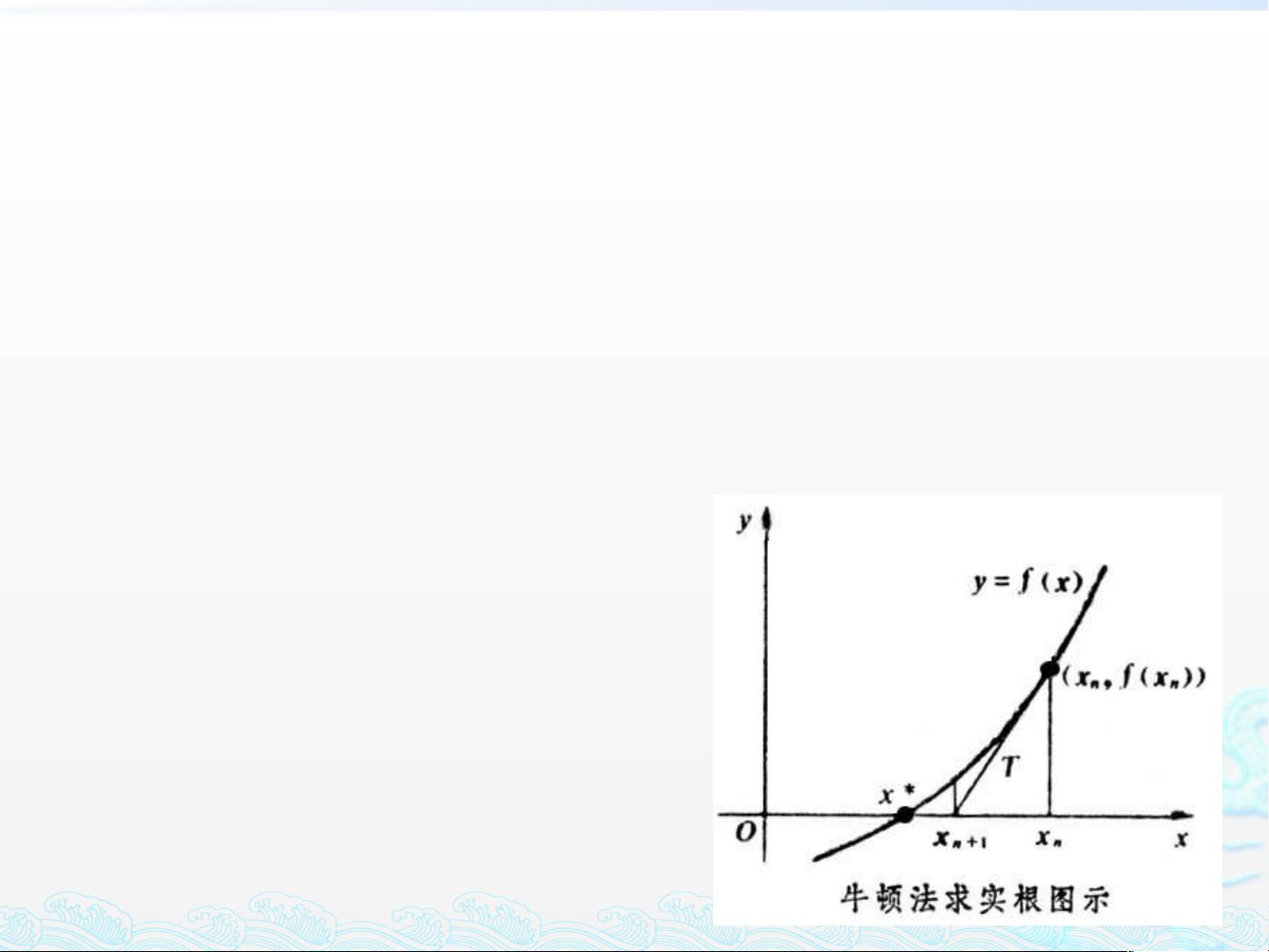
牛顿法与拟牛顿法是优化理论中的核心概念，针对无约束最优化问题提供了高效的求解策略。这两种方法因其快速收敛特性而备受青睐，尤其在解决非线性优化问题时，相较于其他算法如梯度下降法，它们能够提供更精确的解。 牛顿法是一种迭代算法，其基础原理是利用泰勒级数的局部线性逼近，通过构造目标函数在当前点处的二次模型来逼近真实函数。具体步骤如下： 1. 首先，计算目标函数f(x)的一阶导数f'(x)以及二阶导数（海塞矩阵Hessian矩阵）H(x)。 2. 在给定点x_k，构造一元二次函数Q(x) = f(x_k) + f'(x_k)(x - x_k) + (1/2)(x - x_k)^TH(x_k)(x - x_k)，该函数近似了f(x)在x_k附近的值。 3. 求解二次函数的根，即Q(x) = 0，得到下一个迭代点x_{k+1} = x_k - [H(x_k)]^(-1) * f'(x_k)。 4. 重复上述步骤，直到满足停止条件（例如函数值变化小于某个阈值或达到最大迭代次数）。 然而，牛顿法的局限在于每次迭代都需要计算海塞矩阵的逆，这在高维问题中可能导致计算成本显著增加。为了缓解这一问题，出现了拟牛顿法，它通过使用一个正定矩阵来近似海塞矩阵，降低了计算复杂度。拟牛顿法有多种变体，如常用的Broyden-Fletcher-Goldfarb-Shanno (BFGS) 方法，它使用历史信息更新近似矩阵，减少了对真实Hessian的依赖。 在最优化问题中，牛顿法的应用尤为广泛。例如，在非线性规划中，目标函数的极大极小问题可通过寻找导数为零的点来解决，这时牛顿法可以将优化问题视为解方程的问题。对于多变量的情况，牛顿迭代公式扩展为基于Hessian矩阵的高维版本，尽管增加了矩阵操作的复杂性，但它通常能提供更有效的收敛。 在实际应用中，牛顿法因其收敛速度较快而优于梯度下降法，尤其是在函数曲率信息丰富的区域。然而，牛顿法并非总比梯度下降法优越，因为后者在处理大规模数据或稀疏目标函数时更为高效。牛顿法和拟牛顿法是优化工具箱中的宝贵武器，能够在许多数学优化问题中发挥关键作用。