Simulink模拟简谐振动与里沙茹图形分析

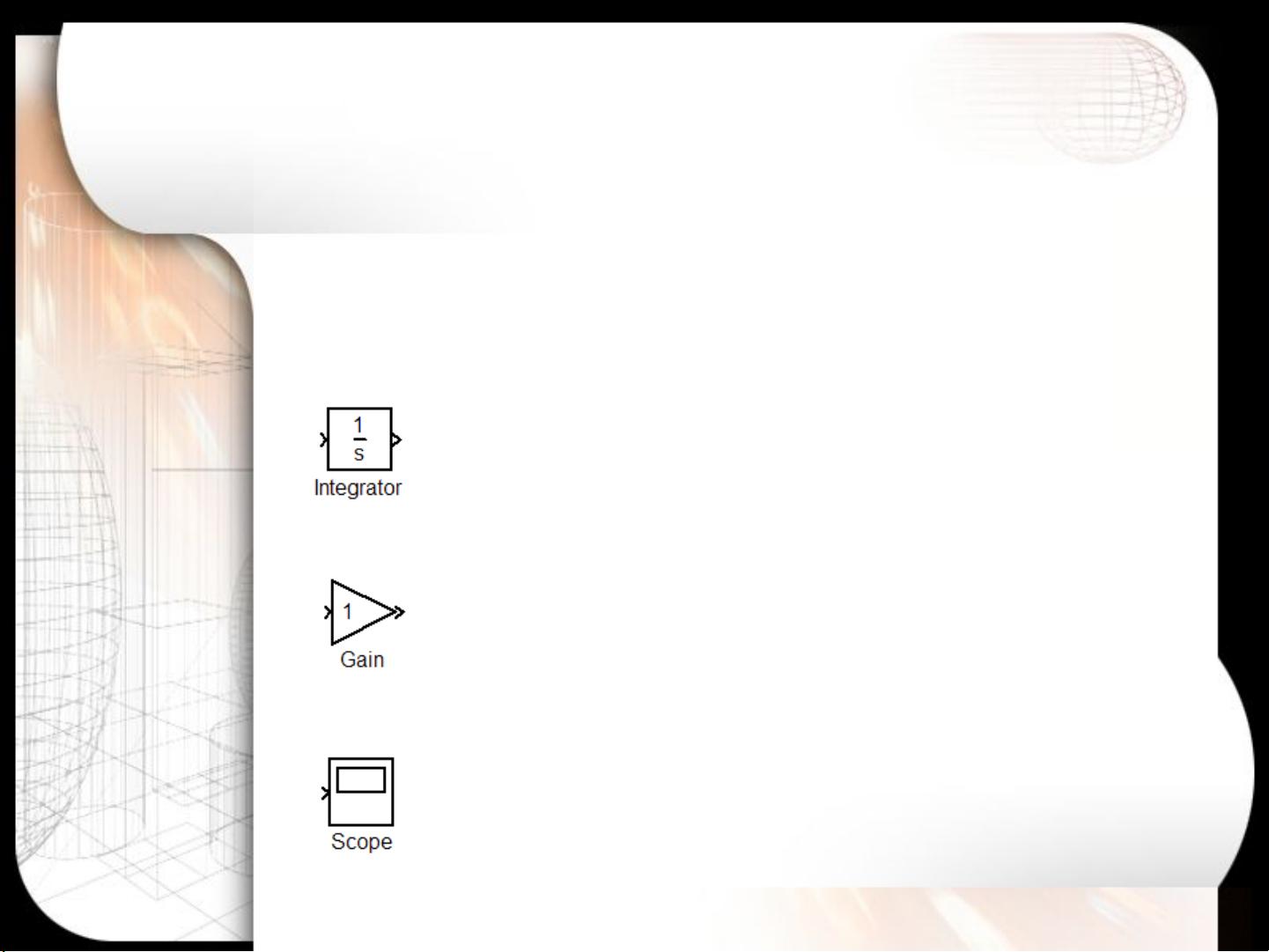
"Simulink机械振动仿真是模拟和分析机械振动现象的一种方法，该实例通过Simulink软件详细展示了单自由度无阻尼振动系统的建模和仿真过程，并介绍了里沙茹图形分析在简谐波形中的应用。" 在Simulink中进行机械振动仿真，我们可以从以下几个方面来理解这个简例： 1. **单自由度无阻尼自由振动**： 单自由度系统通常指的是只受到一个方向约束的振动系统，如弹簧振子。在这个模型中，一个质量m受到弹簧k的作用力，且没有外加阻尼。根据牛顿第二定律，可以得出微分方程：m * x'' + k * x = 0，其中x''代表加速度，x表示位移。在Simulink中，可以通过积分模块（Integrator）来模拟微分方程的解，用乘法器（Multiplexer）来实现力的计算。 2. **模型建立**： 在建立Simulink模型时，需要设定参数，如弹簧刚度k和质量m。本例中，k设为100，m设为10。初始条件是速度为0，位移为1。初始位移可以通过设置积分器的初始条件来设定。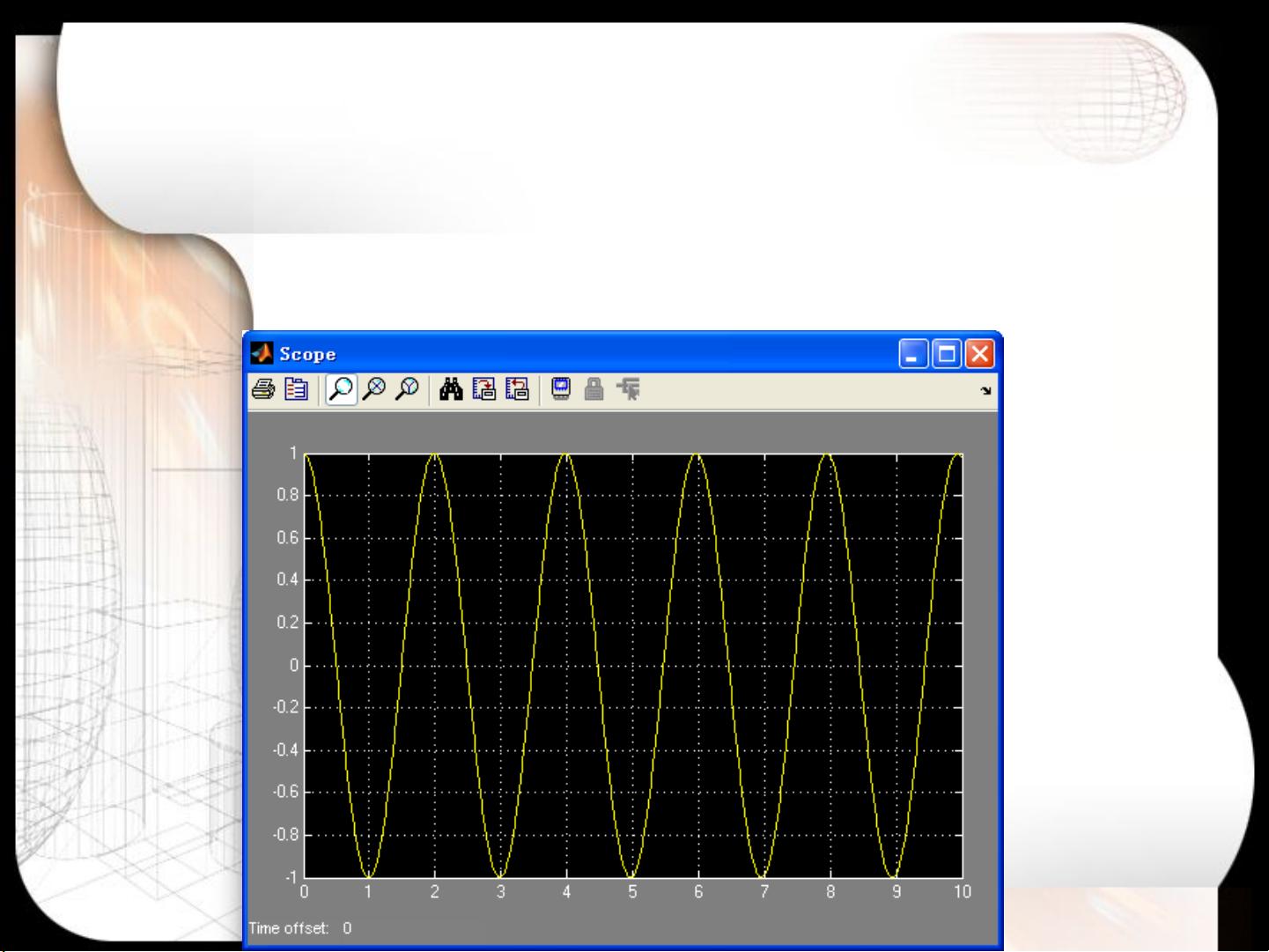 3. **仿真问题与解决**： 初次仿真可能得到的曲线不够平滑，这是因为默认的仿真步长较大。通过减小最大步长（如改为0.01），可以提高仿真精度，使曲线变得平滑。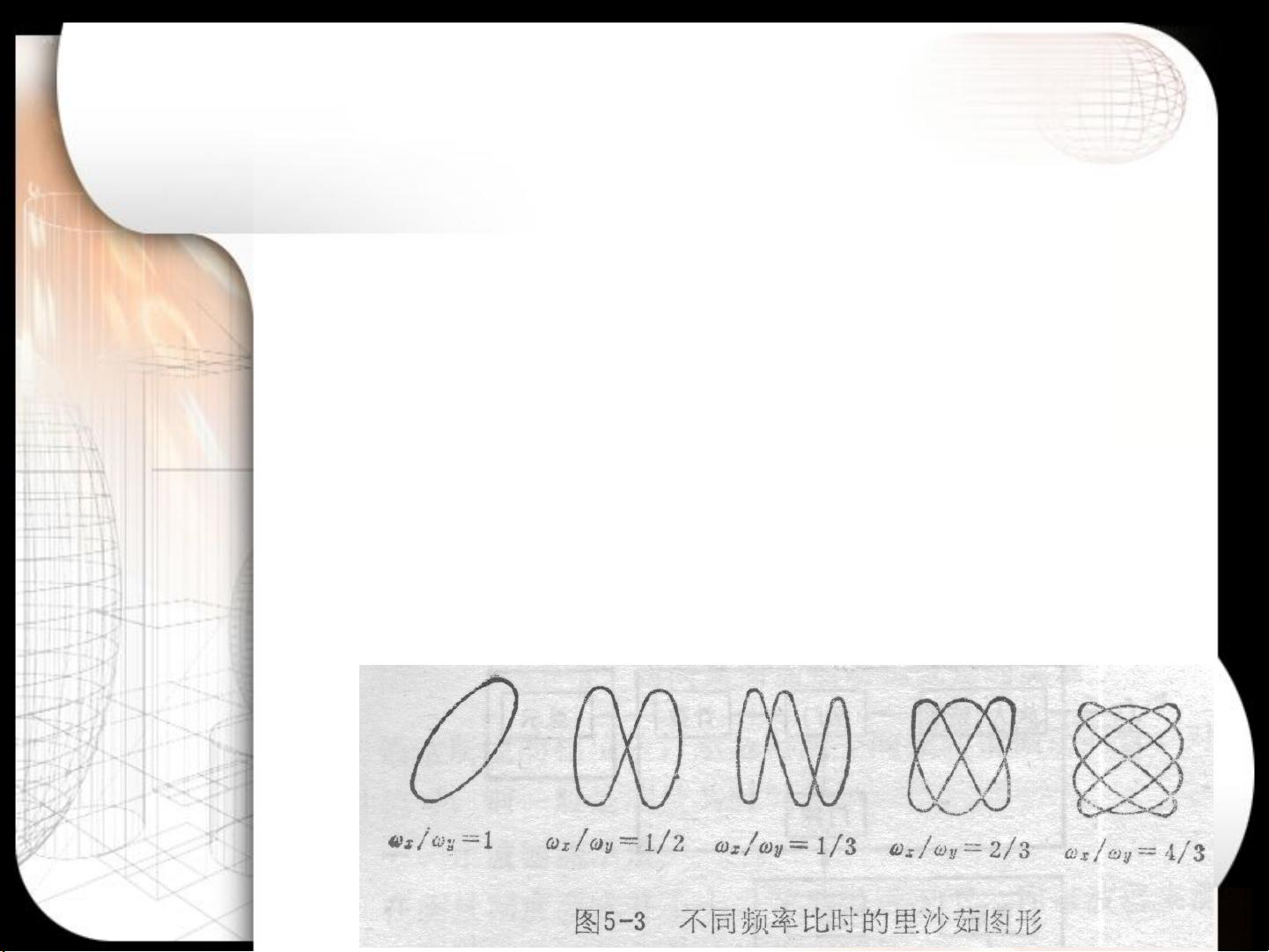 4. **里沙茹图形分析**： 里沙茹图形是一种在示波器上通过叠加两个简谐振动信号产生的稳定轨迹，当它们的频率比是正有理数时，会出现特定的图形。例如，如果频率比为m:n，则轨迹将有m个与y轴的交点，n个与x轴的交点。当两个信号的相位差为90度时，形成的图像为正椭圆。在Simulink中，可以通过示波器模块观察这种合成运动轨迹，有助于理解和分析振动系统的行为。 5. **应用与扩展**： 这个简例不仅展示了基本的单自由度振动系统的仿真，还引入了里沙茹图形分析，这在工程和科研中用于检测和分析振动系统的特性，特别是在信号处理和控制系统设计中具有重要意义。 通过学习这个Simulink机械振动仿真实例，我们可以掌握如何在Simulink环境中构建振动模型，以及如何通过调整参数和观察仿真结果来理解振动系统的动态行为。同时，对里沙茹图形的理解也能帮助我们深入探究信号之间的相互作用和同步现象。