人工智能问题求解与搜索技术解析

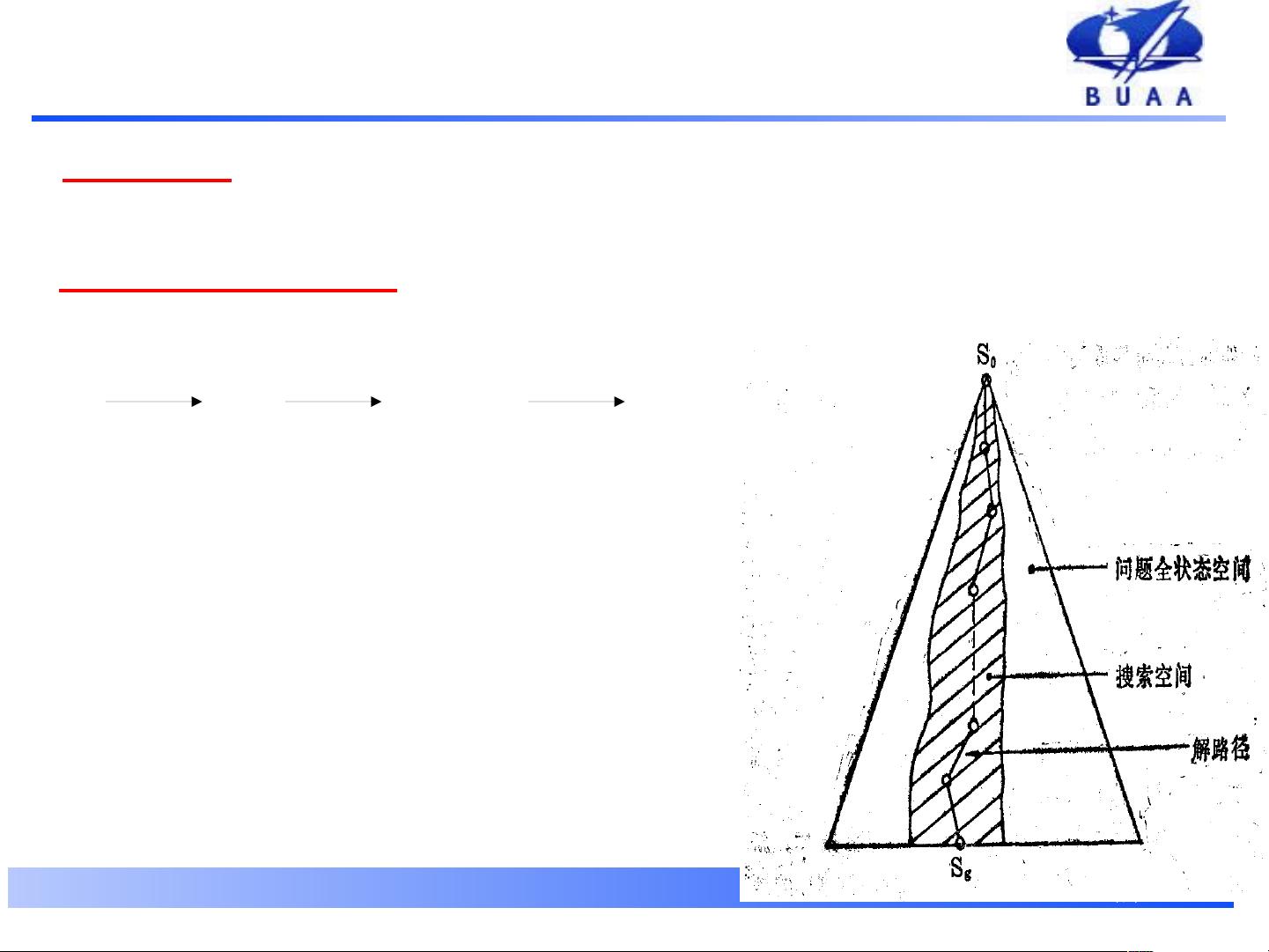
"北航6系人工智能课程的课件，涵盖了问题求解的基本原理及搜索技术。" 在人工智能领域，问题求解是核心概念之一，它涉及到在特定条件下寻找解决特定问题的有效算法。传统软件通常处理的是可以精确数学描述的良结构问题，例如解方程，而人工智能软件则更侧重于解决那些难以直接用数学模型描述的不良结构问题，如几何证明、逻辑演算等。这些问题往往需要利用搜索策略来寻找解决方案。 问题求解的基本方法包括基于状态空间的方法、基于问题空间的方法以及基于博弈搜索的方法。状态空间法是一种常用的技术，它从问题的初始状态开始，通过一系列的状态转换逐步接近目标状态。状态被定义为描述问题中各个元素配置的符号或数据结构，而状态空间则是所有可能状态的集合。在这个集合中，初始状态（S0）和目标状态（G）是明确的，而操作集合（O）则包含了允许的状态转换。 以经典的梵塔问题为例，它是一个典型的状态空间问题。初始状态是所有盘子按照大小顺序堆放在第一根柱子上，目标状态是所有盘子都移动到第三根柱子上，且任何时候大盘子都不能位于小盘子之上。状态空间中的每一步转换都遵循一定的规则，例如，每次只能移动一个盘子，并且不允许大盘子压在小盘子上。通过这种方式，我们可以构建一个状态转换图，通过搜索找到从初始状态到达目标状态的路径。 基于问题空间的方法，又称为递归分解策略，是另一种问题求解方法。这种方法通常用于解决可以分解为子问题的问题，例如，将n个盘子从一根柱子搬到另一根柱子的问题，可以分解为先将n-1个盘子搬到中间柱子，再将最后一个盘子搬到目标柱子，最后再将中间柱子的n-1个盘子搬到目标柱子。这种分解策略遵循一定的合法规则，保证每个子问题的解决都能推动整体问题的解决。 基于博弈搜索的问题求解方法则常用于解决棋类游戏等问题，通过模拟对手可能的走法和自身的最优策略来寻找最佳的下一步。这些方法包括深度优先搜索、宽度优先搜索、启发式搜索等，其中启发式搜索通常结合了问题的特定知识，以提高搜索效率。 在实际应用中，人工智能软件不仅要处理传统的计算任务，还需要处理复杂的数据分析、模式识别、自然语言理解等多种问题。这些都需要利用搜索技术和问题求解策略，结合机器学习、知识表示、推理机制等其他AI领域的技术，共同实现智能决策和自动化问题解决。因此，对问题求解基本原理及搜索技术的理解和掌握对于深入学习和实践人工智能至关重要。