PCA详解：数学模型与Matlab应用实例

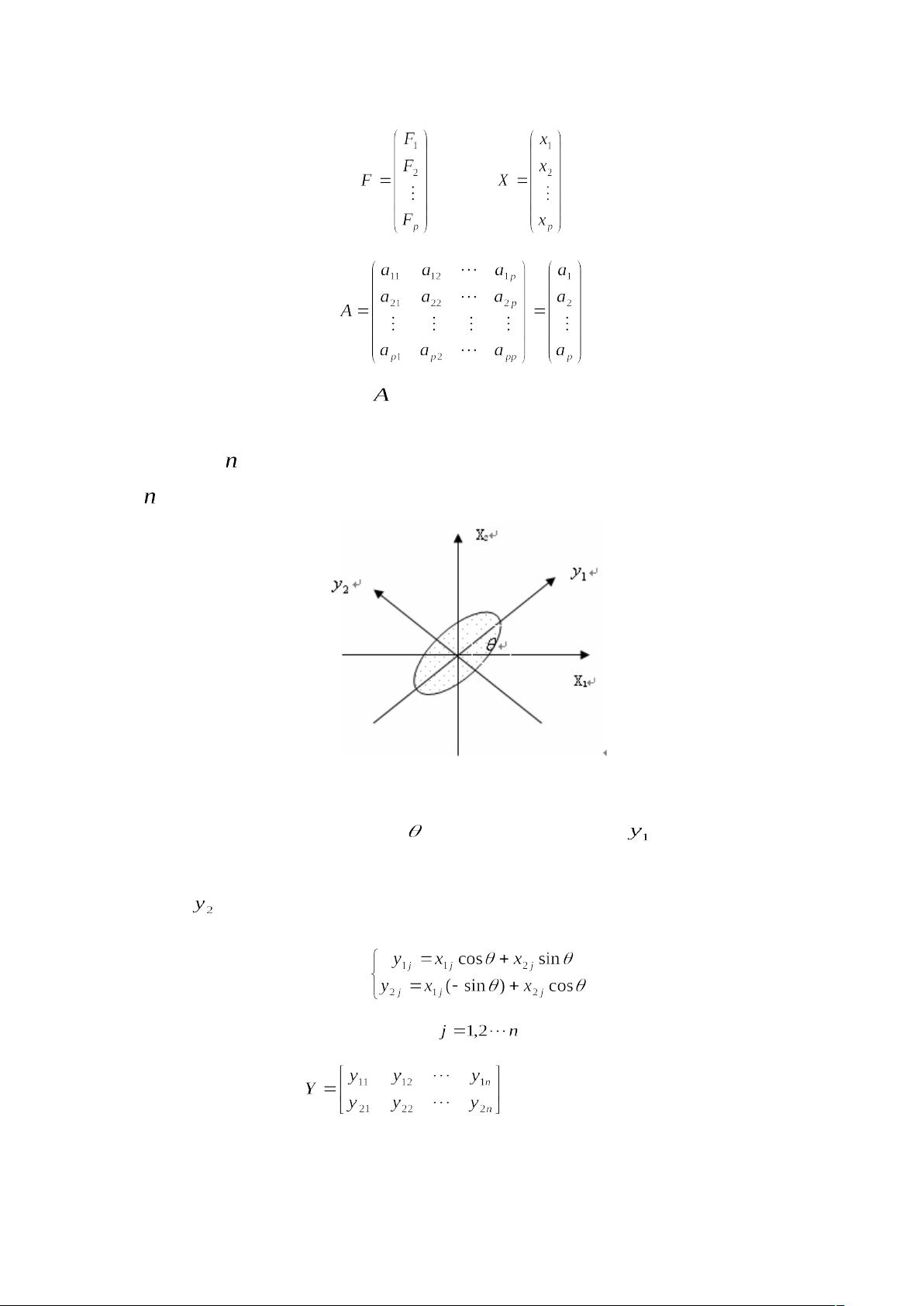
主成分分析(PCA)是一种常用的数据降维技术，主要用于处理多变量数据中的冗余和相关性，以便于提取关键信息并简化复杂的分析过程。PCA的基本思想是通过线性变换，将原始变量集合并转化为一组新的、互不相关的综合变量，这些综合变量被称为主成分。主成分的选择基于对变量信息贡献度的衡量，即方差最大化。 在PCA的数学模型中，我们假设有[pic]个观测变量和[pic]个样品的数据。数据矩阵表示为[pic]，其中每个行代表一个样本，每列代表一个变量。PCA的目标是找到一组新的综合变量[pic]，满足以下条件： 1. **正交性**：新变量[pic]与[pic]之间的相关系数为0，即[pic]，这确保了新变量之间的独立性。 2. **方差排序**：每个新变量的方差按降序排列，即[pic]的方差大于[pic]的方差，以此类推。这意味着前几个主成分包含着大部分的总变异信息。 3. **累计解释方差比**：对于后续的主成分，要求其方差不再包含前一个主成分的信息，即[pic]，这样确保了主成分的独立性。 PCA的具体实现过程包括计算协方差矩阵、特征值分解、选择主成分等步骤。在MATLAB中，可以使用内置的`pca`函数来执行PCA分析，输入数据矩阵，然后根据需要选择保留的主成分数量。 举个例子，假设我们有一个包含多个变量的大型数据集，如股票价格、经济指标等，通过PCA，我们可以提取出影响整体市场波动的主要因素，如市场趋势、宏观经济状况等，从而减少分析的复杂性和数据的噪声。在MATLAB中，可以将数据预处理后，调用`[coeff,score,latent,explained] = pca(data)`，其中`coeff`是主成分系数矩阵，`score`是降维后的数据，`latent`是每个主成分对应的方差，`explained`则展示了每个主成分解释的总变异比例。 通过这种方式，PCA不仅有助于可视化高维数据，还降低了数据分析的难度，使得后续的统计分析更为有效。在实际应用中，如图像处理、生物信息学、金融等领域，PCA都是一个不可或缺的工具。