五边形矩阵解析：平面超对称Yang-Mills理论的新进展

95 浏览量更新于2024-07-16 收藏 468KB PDF 举报

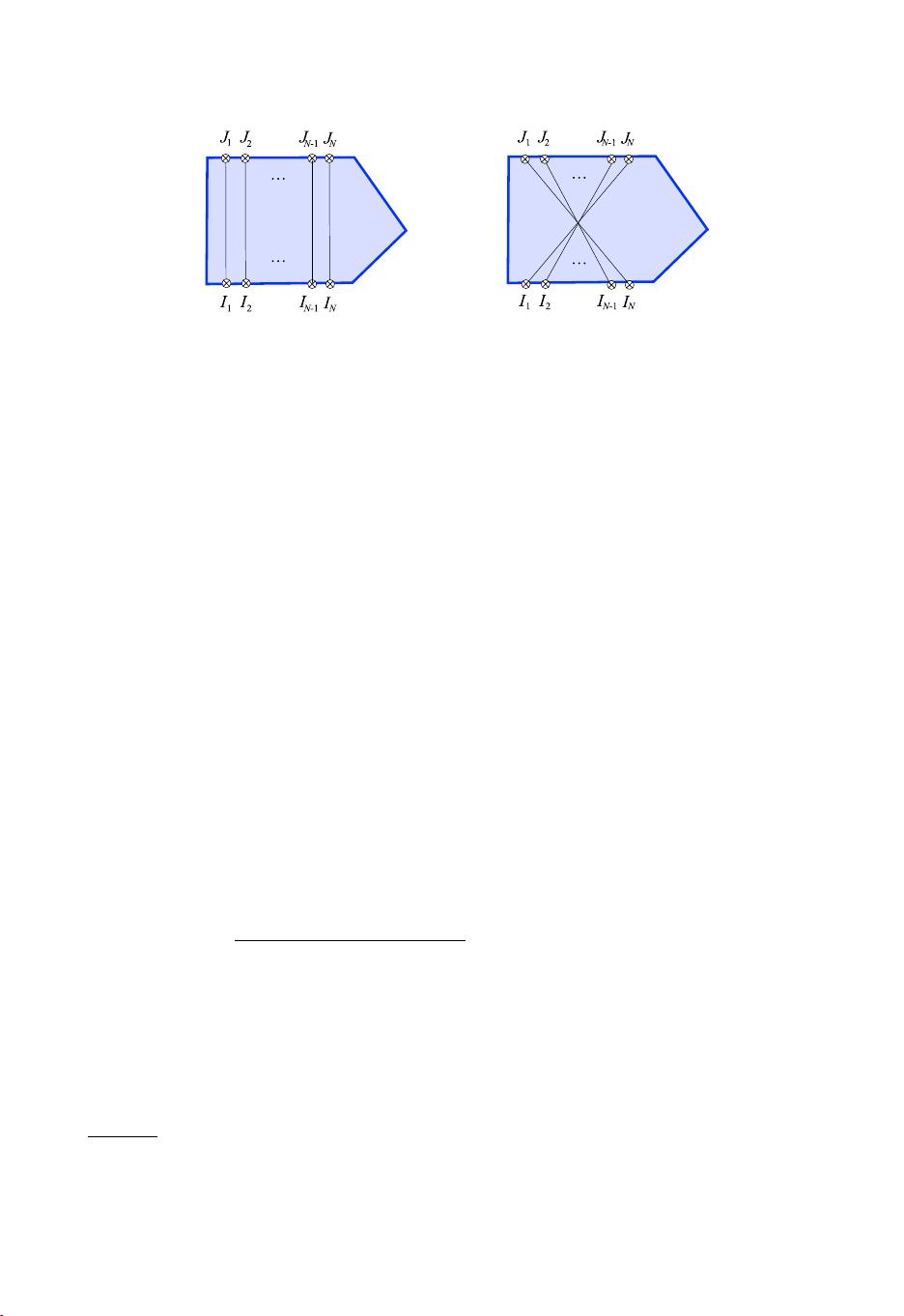
"矩阵五边形——平面极大超对称Yang-Mills理论中的多粒子五边形跃迁与内部对称性的研究" 这篇论文深入探讨了平面极大超对称Yang-Mills理论中的一个重要概念——"矩阵五边形"，这是一种描述零多边形Wilson回路算子积展开的重要工具。在这个理论中，Wilson回路用于研究高能量量子场论中的强相互作用。零多边形 Wilson 回路的算子积展开与多粒子五边形跃迁密切相关，这些五边形表示了色流管上激发物的传播过程，色流管在四维轮廓的两侧终结。过去几年的研究揭示了这种五边形跃迁的动力学特性，但它们的完整描述仍待完善，特别是对于't Hooft耦合的精确依赖关系。在论文中，作者解决了这一问题的关键部分，即SU(4)矩阵结构，这部分是由标量和费米子的内部对称性指标产生的。 SU(4)矩阵结构是理论中不可忽视的一部分，因为它涉及到粒子的内禀性质和相互作用。解决这一难题的方法是通过递归求解所谓的"单重态五边形"遵循的Mirror和Watson方程。这两个方程是数学工具，用于确定五边形跃迁的性质。单重态五边形是指具有特定对称性的五边形，它们在理论中扮演着基础角色。通过解析这些方程并固定张量分解中的扭曲分量，作者能够完整地描述非单价或带电的五边形，这是理解整个理论体系中的关键一步。编辑Stefan Stieberger审阅并接受了这篇论文，它于2017年8月31日在线发布在《核物理学B》第923期，页码588-607。这篇工作不仅深化了我们对Yang-Mills理论的理解，还为未来探索更复杂的多体相互作用提供了重要的理论框架。通过这种方式，矩阵五边形的解析解将有助于物理学家更好地预测和解释高能物理实验中的观测结果。

A.V. Belitsky / Nuclear Physics B 923 (2017) 588–607 591

Fig. 2. Two contributions out of (2N −1)!! of perfect pairings of O(6) indices of holes which are displayed in Eq. (2.4).

The picture on the right shows the twisted graph which corresponds to the seed rational function for the recursive solution

of the deﬁning equations.

2.1. Hole matrices

We start with a comment. The singlet pentagon operator itself obviously does not carry any

SU(4) indices, so its matrix elements can have a total even number of holes shared between the

initial and ﬁnal states. In this section we provide a solution to the diagonal N -to-N case. The

particle number-changing transitions can be deduced from this one making use of the kno

double Wick, aka mirror, transformation properties which allow one to move excitations between

different sides of the pentagon.

With this in mind, let us introduce transitions from the initial state of N scalars carrying

rapidities u = (u

, ..., u

) and O(6) indices

I = (I

, ..., I

), cumulatively called h

(u), to

the ﬁnal state of N scalars h

(v),

I |J

(u|v) =h

(v)|P|h

(u). (2.1)

The above pentagons can be cast in the form of a scalar factor accompanied by an O(6) tensor

I |J

(u|v) = 

I |J

(u|v)P

h|h

(u|v). (2.2)

Here P

h|h

(u|v) contains dynamical information about the transition of N -to-N hole states

through the dependence on the ’t Hooft coupling. It was shown to admit a factorized form in

terms of two-particle pentagons [5,10,13,14]

h|h

(u|v) =



i,j

h|h

)



i>j

h|h

)



i<j

h|h

)

. (2.3)

As was already stated in the Introduction, the matrix 

I|J

(u|v) does not depend on the cou-

pling constant and, as a function of the rapidity variables, it enjoys dependence only through

their differences and is purely rational in nature. Its tensor decomposition runs over (2N − 1)!!

perfect pairings of all indices

We will ﬁnd useful using the SU(4) indices instead when discussing mixed matrix elements. For the time being the

O(6) conventions are the most economical.

We adopt the numbering scheme that naturally emerges from a pairing routine in the accompanying Mathematica

notebook.

剩余19页未读，继续阅读

weixin_38663973

粉丝: 2

五边形矩阵解析：平面超对称Yang-Mills理论的新进展

庞加莱圆盘双曲几何五边形平铺实现与MATLAB开发

MATLAB在对称与非对称五边形系统求解中的应用

2023.08.01 信息学奥赛测试题：Go C 画图与 CSP 竞赛解析

用VC++绘制正五边形

毕业设计MATLAB_求解对称和非对称五边形系统.zip

五边形填充术：栅栏算法的优化技巧与视觉效果分析

五边形填充实战技巧：栅栏算法优化详解（提升渲染效率）

【栅栏填充算法的终极指南】：五边形填充的权威解析与操作秘籍

使用Matlab.用patch函数绘制一个填充渐变色的正五边形

利用 patch 函数绘制一个填充渐变色的正五边形，简单函数即可

最新资源