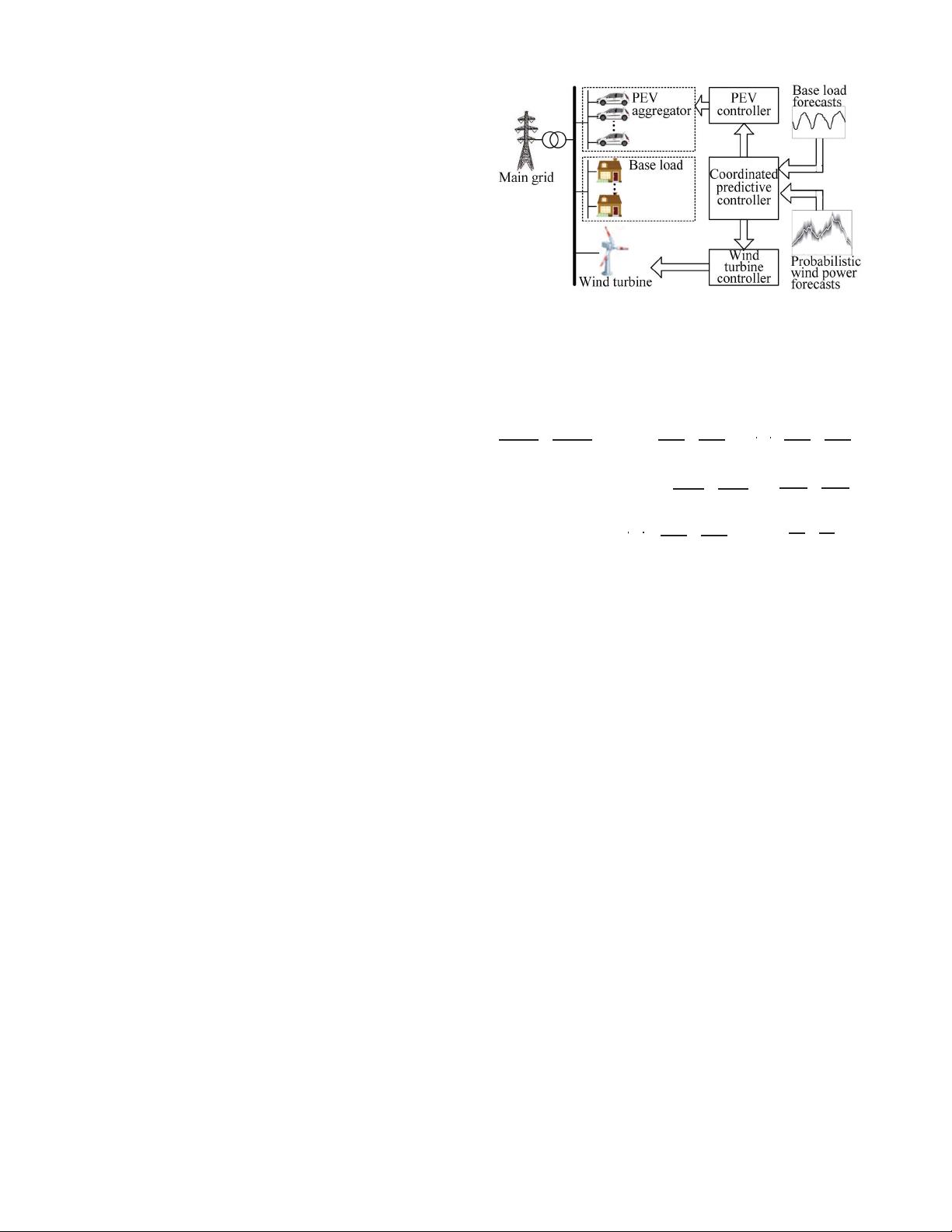
KOU et al.: STOCHASTIC COORDINATION OF PEVs AND WIND TURBINES IN MICROGRID 1539
a desired trajectory. To address this, the proposed scheme uses
a target zone as the power reference for wind turbine, rather
than a traditional reference trajectory.
The remainder of this paper is organized as follows.
Section II presents the mathematical model of the microgrid,
PEV aggregator, and wind turbine. Section III gives the precise
control problem formulation and the detailed description of the
proposed control scheme. Section IV contains the description
of the simulations and the discussion of the results. Finally,
Section V draws the conclusions.
II. M
ODELING OF WIND-PEV MICROGRID
A. Microgrid Layout and Modeling
In this paper, we consider a microgrid with a DFIG wind tur-
bine and several PEVs, as well as general user demands (i.e.,
the baseline load profile without PEV loads). A schematic rep-
resentation of the considered microgrid is shown in Fig. 1.This
microgrid is connected to the main grid through a transmission
line. It is expected that the power exchange between the micro-
grid and main grid is minimized, i.e., the power generation
matches the demand in this microgrid.
Based on the layout shown in Fig. 1, an overall linear
dynamic model for the microgrid can be formulated as follows:
E
V ,agg
(k
M
+ 1) = E
V ,agg
(k
M
) + ηυP
V ,agg
(k
M
)
+ E
V ,arr
(k
M
) − E
V ,leav
(k
M
)
P
G
(k
M
) = P
W
(k
M
) − P
V ,agg
(k
M
) (1)
where k
M
is the index of time slot, each time slot is 15 min.
In this paper, we only consider the private PEVs, i.e.,
private-owned PEVs. The driving pattern of these PEVs is
relatively flexible and they are usually not in use for most
of the time in a day, especially during the night. Therefore,
these PEVs are suitable candidates of flexible energy storage
facilities, which can be used to absorb the surplus wind power
and improve the power balance during the off-peak times at
night [10]. For this reason, the time horizon of the proposed
control scheme is 6:00
P.M.to6:00A.M. Similar to the settings
in [15], in this paper, it is assumed that some private PEVs
will voluntarily be registered as dispatchable PEVs during the
night. To achieve this, associate payments can be made to
attract the owners to register their PEVs. Once registered, the
owners of PEVs should guarantee that their PEVs are plugged-
in during the night. In this way, the microgrid operator can
then use these dispatchable PEVs as flexible energy storage
facilities and dispatch them if necessary. Of course, even with
associate payments, during the night, some PEV owners may
still leave home and disconnect their PEVs from the V2G
discharging facility. In our setting, this scenario is regarded
as additional noise E
V ,leav
(k
M
), which will be discussed in
detail later.
In previous wind-PEV dispatching studies, the wind turbine
power output P
W
is normally regarded as a deterministic vari-
able, and hence, the uncertainties in wind power are neglected.
Nevertheless, as discussed in Section I, such uncertainties
significantly affect the control performance. To address this,
unlike previous works, we regard P
W
as a stochastic variable
Fig. 1. Schematic representation of the microgrid, together with the proposed
hierarchical control scheme.
in this paper. Consequently, the state space form of this linear
dynamic model can be expressed as
E
V ,agg
(k
M
+ 1)
x
M
(k
M
+1)
=
[
1
]
A
M
E
V ,agg
(k
M
)
x
M
(k
M
)
+
[
ηυ
]
b
M
P
V ,agg
(k
M
)
u
M
(k
M
)
+
[
1
]
b
M
E
V ,arr
(k
M
)
z
E
(k
M
)
−E
V ,leav
(k
M
)
z
N
(k
M
)
y
M
(k
M
) =
[
−1
]
c
M
P
V ,agg
(k
M
)
u
M
(k
M
)
+
[
1
]
c
M
P
W
(k
M
)
z
W
(k
M
)
. (2)
In model (2), P
V ,agg
is taken as the control input, P
W
and
E
V ,arr
are modeled as the additive stochastic disturbance z
W
and z
E
, respectively. The energy stored in leaving PEVs is
modeled as white Gaussian noise z
N
. The statistics of z
W
and z
E
will be discussed later.
B. PEV Aggregator Modeling
In the microgrid model (2), the PEV aggregator is modeled
by the stochastic variable E
V ,arr
(k
M
), i.e., the energy stored
in the PEVs that arrive home during the k
M
th time slot. This
variable is regarded as a disturbance to the system, so we
need to estimate its value in the controller design. To achieve
this, we derive an estimation model for E
V ,arr
(k
M
) in this
section. In this paper, the total number of PEVs is assumed
to be 300.
Specifically, E
V ,arr
(k
M
) is a function of the number of
PEVs that arrive home during the k
M
th time slot as well as the
initial energy in each PEVs battery at the time of plug-in. In
the following discussions, these two quantities are denoted by
N
V ,arr
(k
M
) and E
V ,arr,j
(k
M
), respectively. Considering the
stochastic nature of the PEV driving pattern, we derive statis-
tical models for these two quantities based on the data in [17].
These data are obtained from the real-world driving database
in Southeast Michigan.
Based on this driving behavior data, the statistical model
of N
V ,arr
(k
M
) can be obtained using the maximum like-
lihood estimation and curve-fitting techniques. Specifically,
we find that before 12:00
P.M., N
V ,arr
(k
M
) can be modeled
by truncated Gaussian distributions, as in Fig. 2. By 12:00
P.M., almost all PEVs arrive home. Moreover, as mentioned
before, we assume that the time horizon of the proposed con-
trol scheme starts at 6:00
P.M. Considering these facts, from



















