离散时间信号与系统分析：Z变换及应用

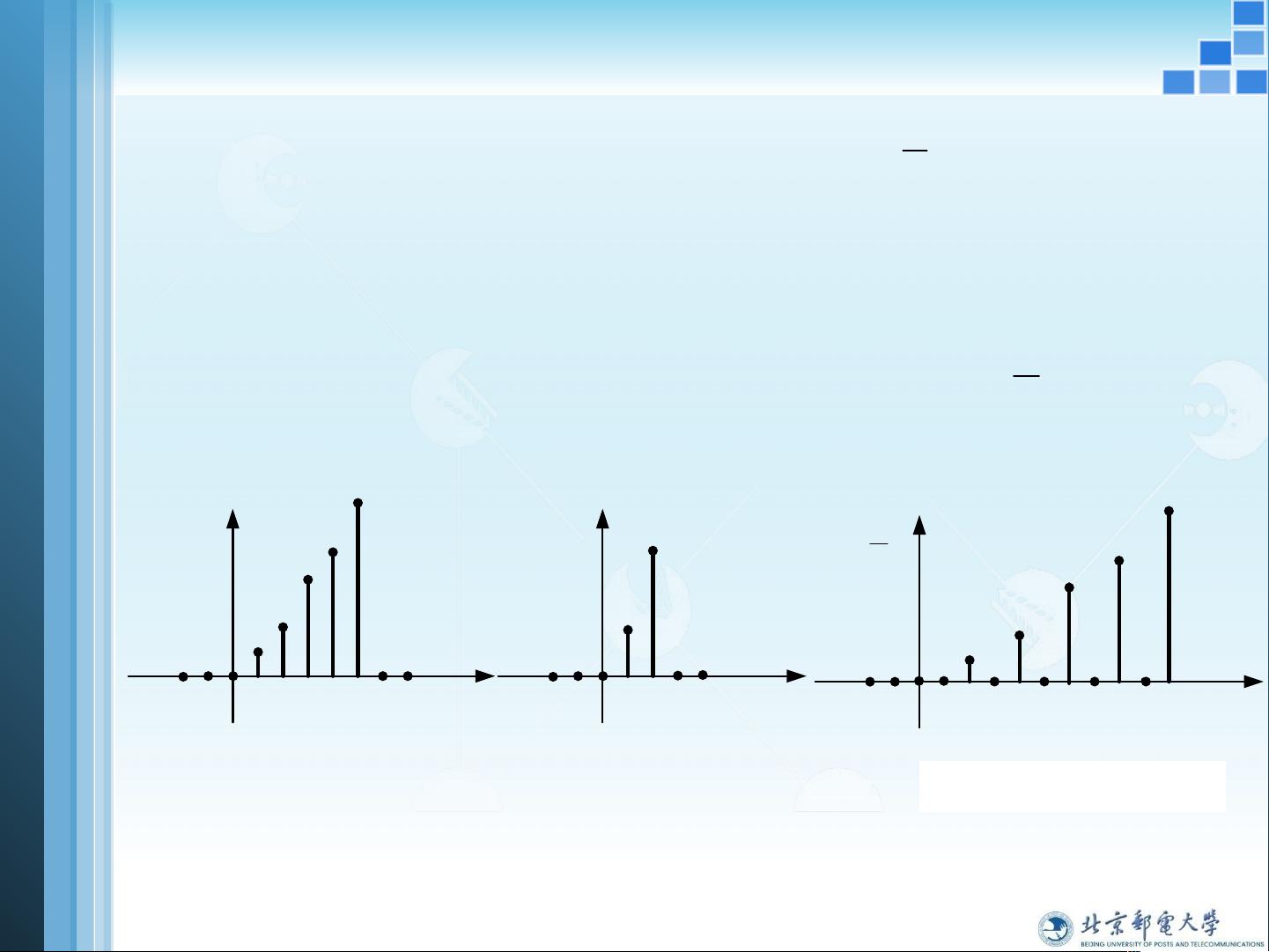
"该资源是关于通信技术基础理论的第六章——离散时间系统的分析，内容涵盖离散时间信号的时域表示、序列的基本运算、典型序列、离散时间系统的数学模型、离散卷积、z变换以及其性质。文件以PPT的形式详细讲解了数字通信的优势与模拟通信的缺点，并通过实例介绍了序列的相加、相乘、移位和标度变换等操作。" 离散时间信号与系统是通信技术中的核心概念，特别是在数字信号处理领域。第六章主要探讨了以下几个知识点： 1. **离散时间信号的时域表示**：离散时间信号是由一组样值组成的序列，通常用集合形式表示，如xn。为了明确位置，序列通常会在n=0处标注小箭头。离散信号可以通过波形或线段的长短来表示数值的大小。 2. **序列的基本运算**： - **相加**：对应序号的样值相加，形成新的序列。 - **相乘**：对应序号的样值相乘。 - **移位**：序列可以向左或向右移位，改变样值的位置。 - **标度变换**：序列乘以常数a，可以实现信号的压缩或扩展。 3. **离散时间系统及其数学模型**：离散时间系统处理离散时间信号，其数学模型常使用差分方程或z变换来描述。 4. **z变换**：z变换是离散时间信号分析的重要工具，类似于连续时间信号的拉普拉斯变换。它将离散时间信号转换到Z域，便于分析系统的性质和求解系统响应。 5. **z变换的性质**：z变换有多个重要的性质，包括线性性、时间平移、尺度变换等，这些性质使得处理离散时间信号更为方便。 6. **模拟信号与数字信号**：模拟信号直观易实现，但保密性和抗干扰能力较差；数字信号具有抗干扰强、便于加密、存储和处理等优点，但需要更宽的频带、更高的同步精度，并可能引入量化误差。 7. **离散卷积**：用于求解离散时间系统的零状态响应，是序列运算的一种特殊形式。 通过这个资源，学习者能够深入理解离散时间信号的表示方法、运算规则以及如何利用z变换分析离散时间系统。实例和习题的提供有助于巩固理论知识，并提升实际应用能力。