理解RC电路瞬态响应：脉冲波形与时间常数探索

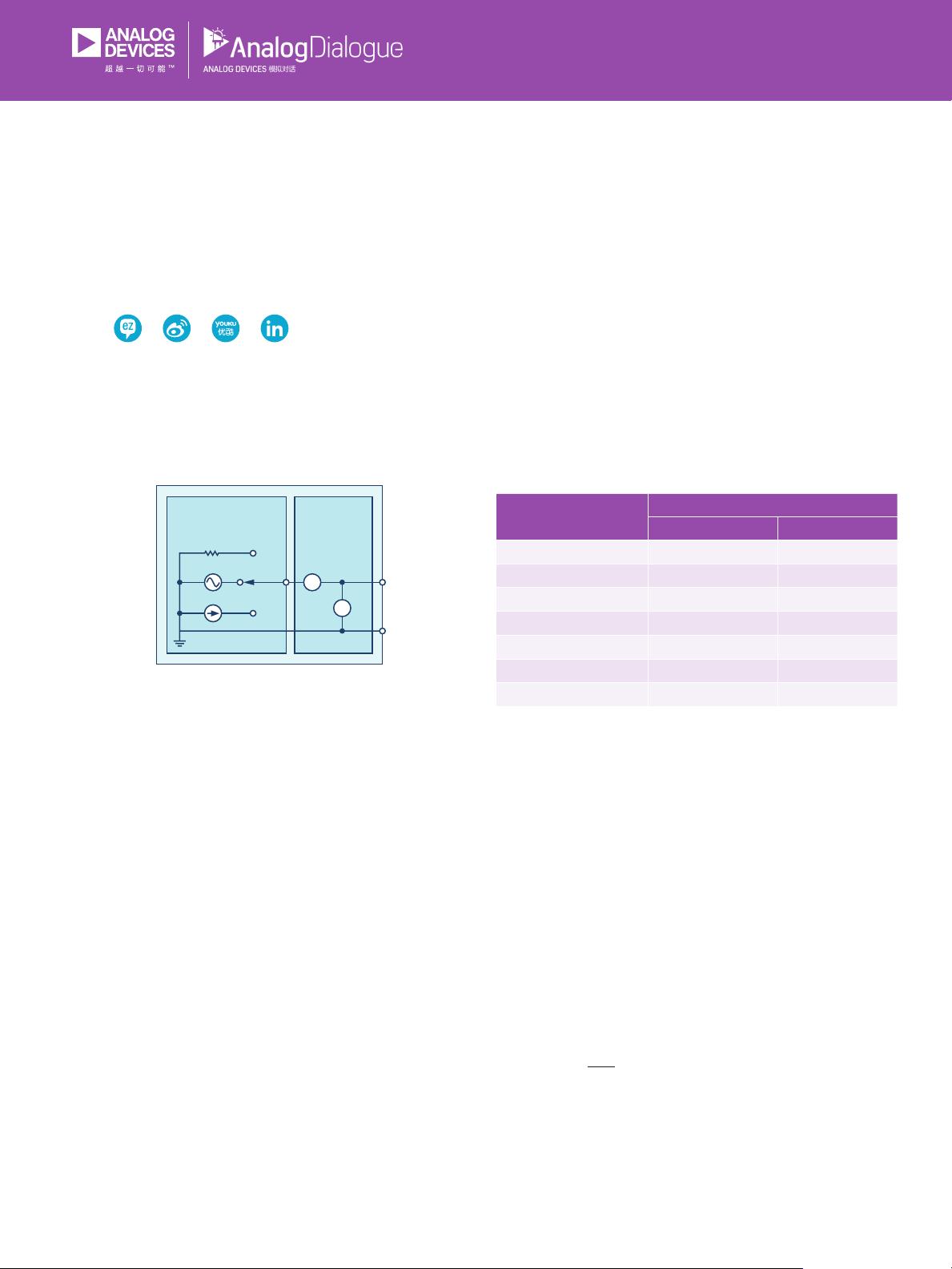
"RC电路的瞬态响应.pdf" RC电路，全称电阻-电容电路，是一种常见的电子电路，由电阻和电容串联组成。在电路理论中，RC电路的瞬态响应是研究的重点，因为它揭示了电路在输入信号变化时电压和电流如何随时间演变。在本实验中，通过向串联RC电路施加脉冲波形，可以直观地观察到这种瞬态响应。 目标是利用脉冲波形分析串联RC电路的瞬态响应，同时理解时间常数（τ）的概念。时间常数是RC电路的一个关键参数，它定义了电路对输入变化的响应速度。在RC电路中，时间常数τ等于电阻R与电容C的乘积，即τ = R × C。这个时间常数决定了电容充电或放电的速度。 在脉冲宽度与时间常数的关系中，当脉冲宽度接近或大于4τ时，电容上的电压会达到约98%的最大值，这被认为是瞬态响应的结束。而超过5τ时，电路进入稳态响应，此时电压和电流趋于稳定值。表1展示了在不同时间常数下，RC充电电路中电容的电压和电流百分比。 脉冲波形是电压或电流的突然变化，随后回到原始水平。方波脉冲是其中的一种，其高电平时间和低电平时间相等，周期T为一个脉冲循环的长度。理想方波的脉冲宽度tp等于周期T的一半。脉冲宽度和频率f的关系由公式f = 1/(2tp)给出。 实验材料包括ADALM1000，这是一个微波实验室模块，可用于进行基本测量，如在本实验中分析RC电路的瞬态响应。通过这个设备，学生和工程师可以直观地了解RC电路的工作原理，并掌握时间常数对电路性能的影响。 在实际应用中，RC电路广泛用于滤波、延时、积分和微分电路等。理解瞬态响应和时间常数对于设计和调试这些电路至关重要。通过这样的实验活动，参与者能够加深对基本电路理论的理解，并提升实际操作技能。