数字信号处理技术在测量频率响应和有效位数中的应用

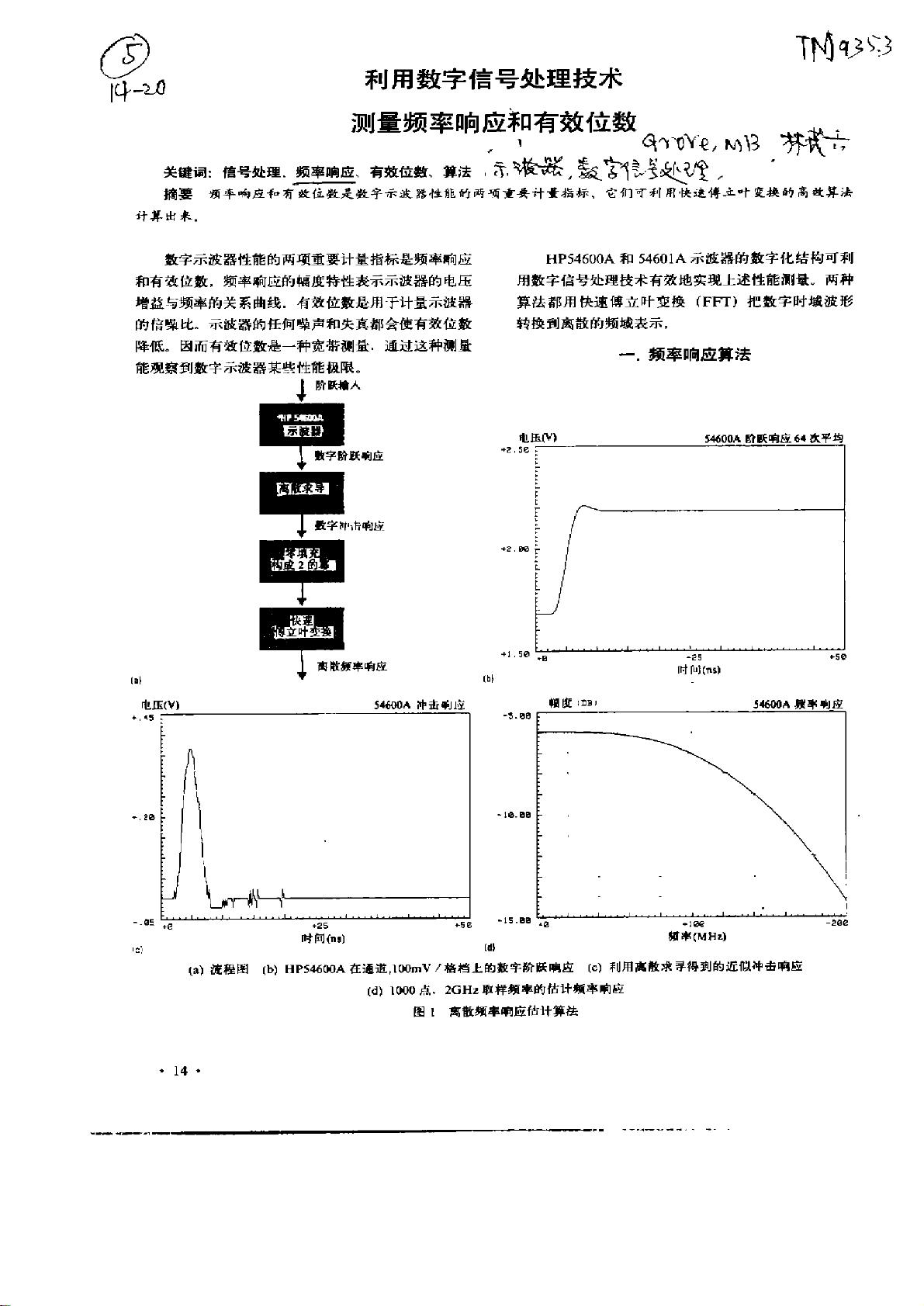
"本文主要探讨了如何利用数字信号处理技术来测量频率响应和有效位数，特别是针对HP54600A和54601A示波器的性能测试。通过使用快速傅立叶变换(FFT)算法，可以将数字时域波形转化为频域表示，从而进行频率响应的测量。文章提到了阶跃响应和冲击响应的概念，并解释了它们在测量过程中的应用。此外，还讨论了误差来源和如何通过平均模式减少噪声的影响。" 在数字信号处理领域，测量频率响应和有效位数对于评估示波器等电子设备的性能至关重要。频率响应是指设备对不同频率信号的电压增益，它描述了设备的幅度特性。而有效位数则用来衡量示波器的噪声和失真水平，这些因素会降低测量的精度。有效位数的测量通常涉及宽带分析，因为它能够揭示设备在宽频率范围内的表现。 文章中提到了HP54600A和54601A示波器，这两款设备的数字化架构使得它们能够高效地进行性能测试。使用FFT算法，可以将捕获的数字时域波形转换为频域表示，从而计算出频率响应。首先，通过阶跃响应测试，即向示波器输入一个阶跃信号，记录其输出，然后通过对阶跃响应求导得到冲击响应。冲击响应的傅立叶变换即为频率响应。图1展示了这一过程，包括阶跃响应、冲击响应和估计的频率响应。 在实际操作中，离散求导可能会引入噪声，可以通过设置示波器的平均模式来减少这种噪声。另外，由于FFT算法要求点数为2的偶次幂，因此可能需要在波形末尾填充零，但这不会显著影响频率响应的准确性。 然而，测量过程中存在一些误差源，如阶跃输入本身可能导致误差，因为实际的频率响应是阶跃输入响应与示波器固有频率响应的乘积。此外，离散处理过程中的量化误差、采样率限制以及噪声都会影响测量精度。了解这些误差来源可以帮助优化测量方法，最大限度地减小误差。 利用数字信号处理技术测量频率响应和有效位数是一项复杂但必要的任务，它涉及到信号处理理论、频域分析和误差控制等多个方面。通过深入理解这些概念和技术，可以更准确地评估和优化示波器等电子设备的性能。