汉诺塔问题解决：递归算法在Java中的实现

"这篇文档详细介绍了使用面向对象程序设计方法解决汉诺塔问题的过程，主要语言为Java。文章首先介绍了汉诺塔问题的背景和历史，然后重新阐述了问题的具体要求，接着进行了算法分析，使用了递归的思想来解决。在程序设计部分，通过流程图和模块功能介绍展示了如何实现这一算法。最后，对运行结果进行了调试，并分析了算法的时间复杂度。" 一、背景知识 汉诺塔问题源于中东的一个古老传说，涉及到三个钻石宝塔，目标是将一个塔上的所有盘子借助另外两个塔，按照特定规则移动到另一个塔上。这个问题由19世纪的法国数学家鲁卡研究，计算出完成任务需要的移动次数极其庞大。 二、问题重述 问题简化为三个柱子A、B和C，A柱子上有n个编号从大到小的盘子。目标是借助C柱，将所有盘子移到B柱，每次只能移动一个盘子，且大盘子不能覆盖在小盘子上。 三、算法分析 解决汉诺塔问题的关键在于递归算法。基本思路是：先将A柱上除最底部盘子外的n-1个盘子借助C柱移动到B柱，再将A柱上的最底部盘子直接移动到C柱，最后将B柱上的n-1个盘子借助A柱移动到C柱。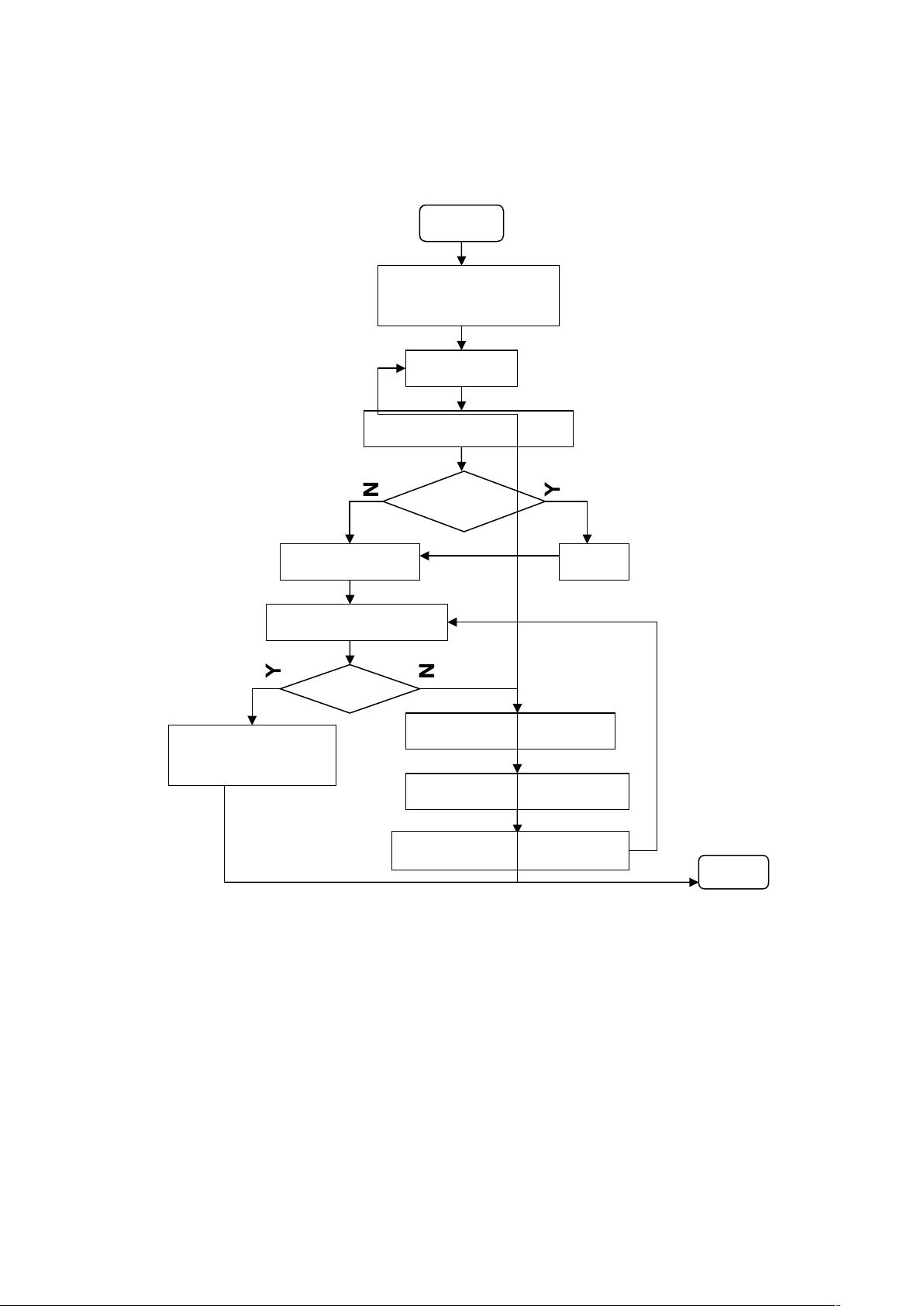 四、流程及程序设计 1. 流程图：通常会描绘出递归调用的过程，展示如何通过反复移动n-1个盘子来实现整个盘子的转移。 2. 模块及其功能介绍：程序可能包含一个主函数，负责启动递归过程；一个递归函数，处理盘子的移动；以及可能的辅助函数，用于打印状态或验证移动合法性。 五、调试与算法复杂度分析 1. 运行结果：程序运行后，应能观察到盘子按照预期规则正确移动到目标位置。 2. Hanoi塔问题复杂度分析：由于每次移动都需要进行2^n-1次操作，因此时间复杂度为O(2^n)，其中n是盘子的数量。对于较大的n值，这意味着算法效率较低。 总结：本文档提供了面向对象编程解决汉诺塔问题的全面解析，通过理解递归思想和实际代码实现，读者可以学习到如何用Java进行高效的算法设计。