动态规划算法详解：0/1背包问题与实例

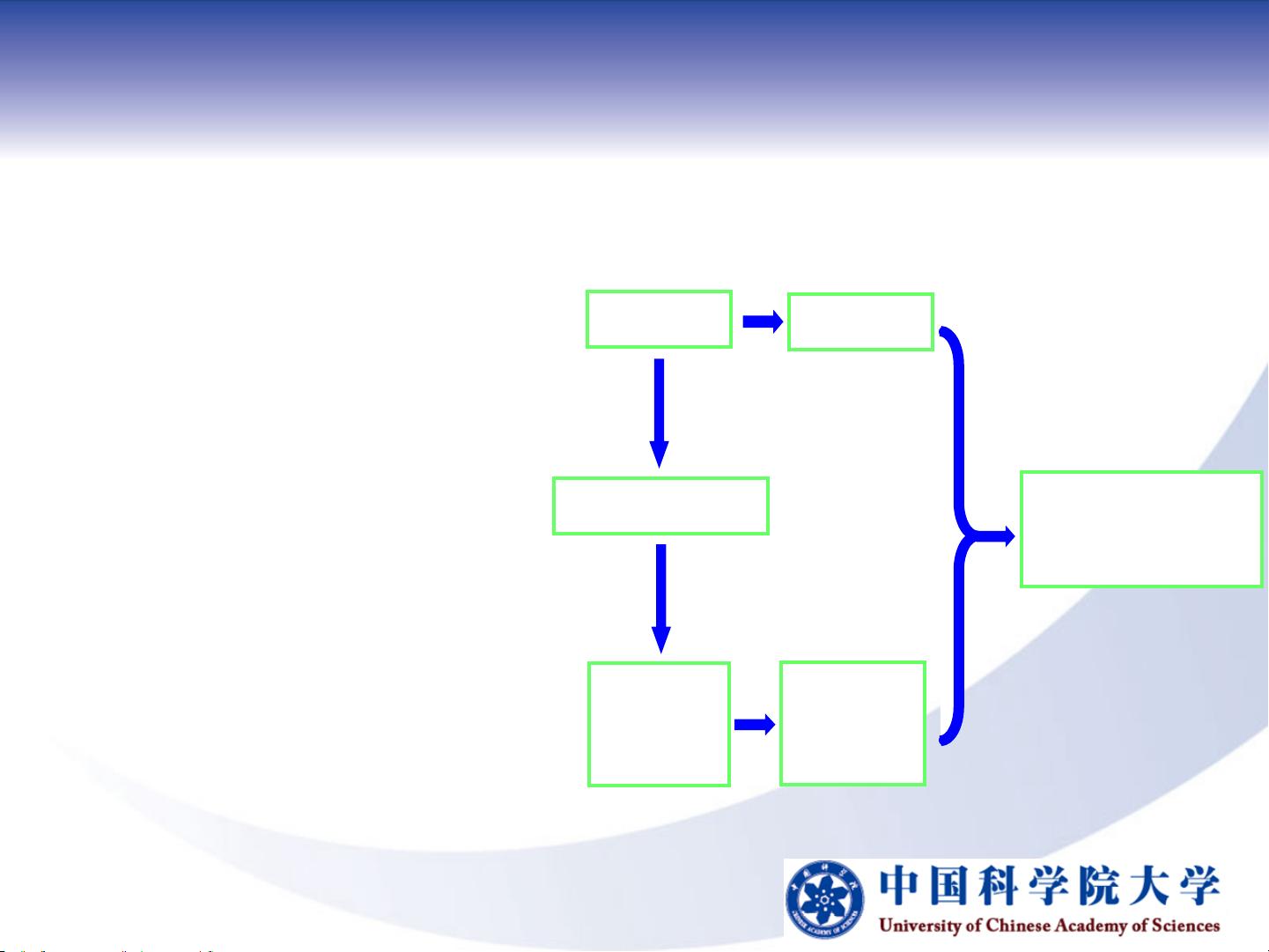
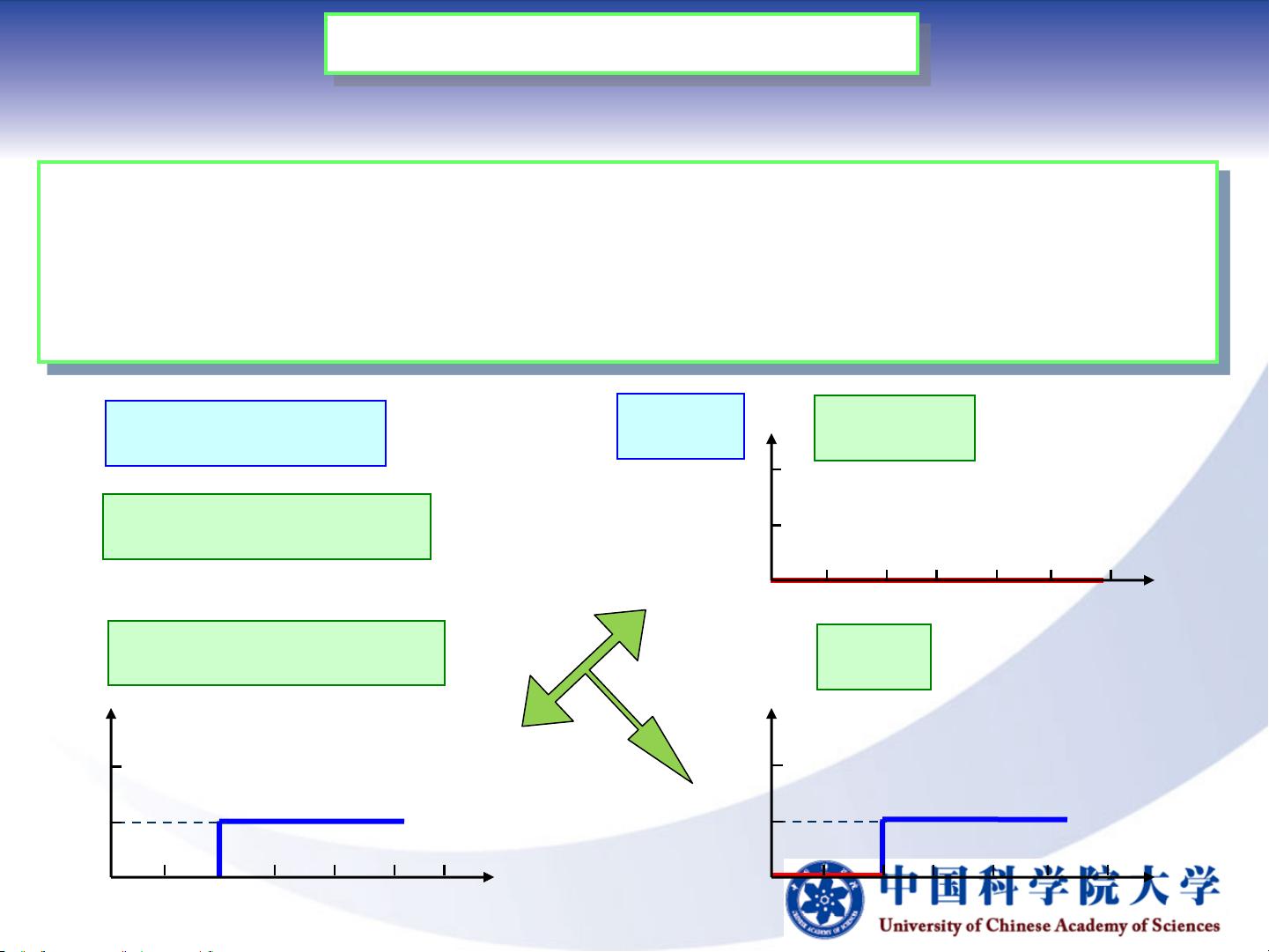
第五章动态规划是《计算机算法设计与分析》中的核心内容，由马丙鹏在2020年10月22日编写。本章详细探讨了动态规划这一重要的算法设计技术，它主要用于解决具有重叠子问题和最优子结构的问题。以下是本章涵盖的主要知识点： 1. **一般方法**：介绍动态规划的基本思想和步骤，包括将大问题分解成更小的子问题，并存储子问题的解以避免重复计算。 2. **多段图问题**：讨论涉及多个部分的图问题，如网络流、图的最短路径等，动态规划在这里用于找到各个部分的最优解决方案组合。 3. **每对结点之间的最短路径**：讲解如何通过动态规划求解最短路径问题，比如Dijkstra算法或Floyd-Warshall算法，以找到网络中任意两个节点之间的最短路径。 4. **最优二分检索树**：这是一种特殊的数据结构，通过动态规划构建，用于高效地搜索和插入元素，同时保持查询性能。 5. **0/1背包问题**：这是经典的动态规划问题，涉及物品分配决策，每个物品有一个重量和一个价值，目标是在不超过总容量的情况下，选择物品以最大化总价值。问题描述了目标函数和约束条件，以及两种递推策略——向前递推（自底向上）和向后递推（自顶向下）。 - 向后递推关系式给出了求解最优解的递归公式，例如，fn(M)表示在容量M下包含前n个物品的最大价值，可以通过更新函数来逐步计算。 - 初始状态和边界条件是关键，例如f0值通常是负无穷，而fj(X)的递推规则展示了如何根据前一个状态和当前物品的价值和重量来决定是否包含该物品。 6. **可靠性设计**：动态规划在可靠性工程中的应用，涉及系统故障概率分析和优化设计。 7. **货郎担问题**：另一种优化问题，类似于0/1背包问题，但可能涉及到多个位置的物品分配。 8. **流水线调度问题**：动态规划用于优化任务在多步骤流水线上的执行顺序，以最小化总完成时间或最大化生产效率。 例1背包问题是一个具体的0/1背包问题实例，通过递推计算展示如何运用动态规划策略解决实际问题，包括确定哪些物品应该放入背包，以及在给定总容量限制下的最大价值。 第五章动态规划深入剖析了动态规划算法在解决各种复杂问题中的核心应用，通过一系列实例演示了如何设计和应用这些算法来求解最优化问题。掌握动态规划是理解和设计高效算法的关键，对于计算机科学和信息技术领域的学习者来说至关重要。