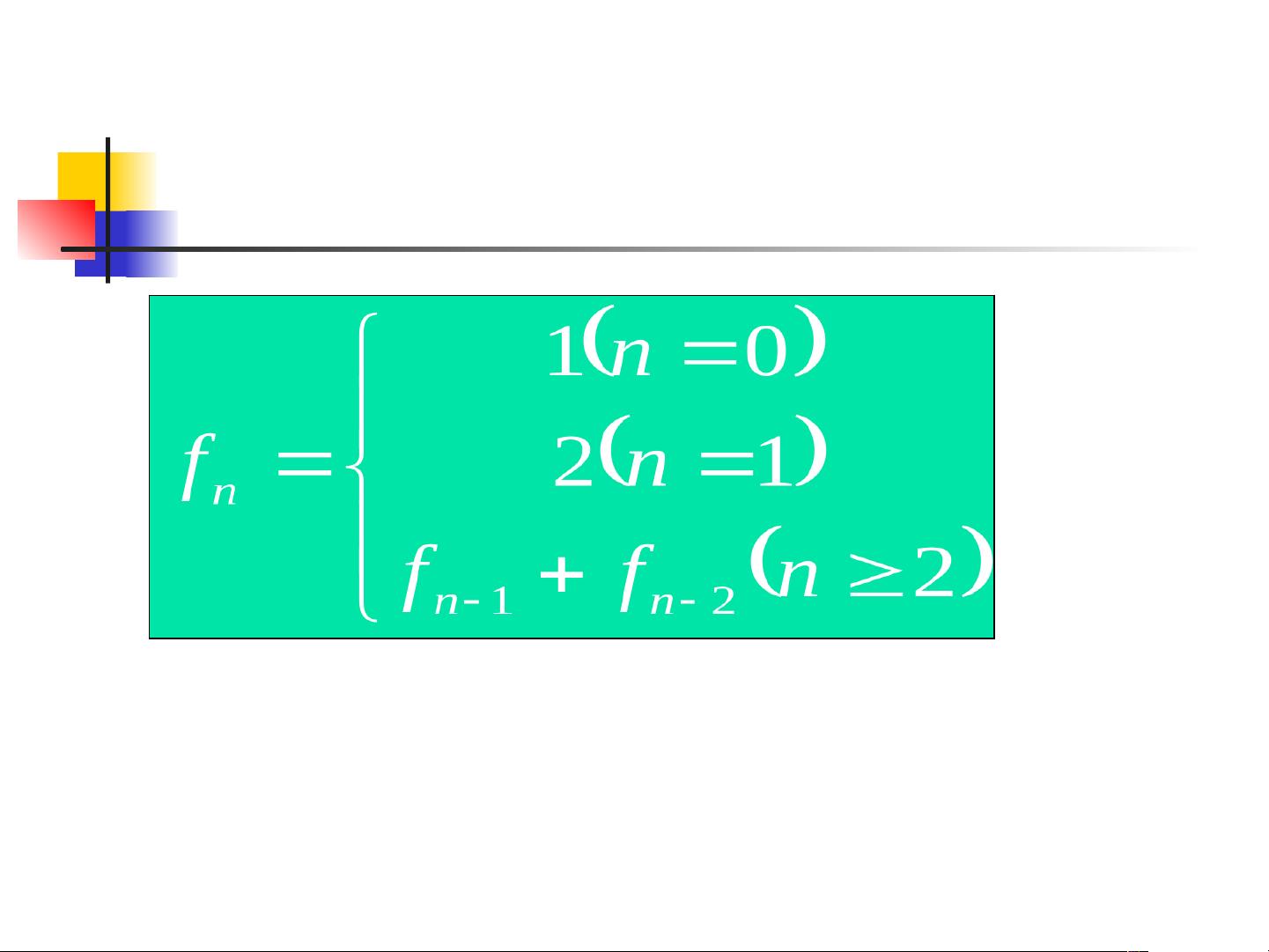递推求解在ACM程序设计中的应用

"这篇内容是关于杭电ACM课程中的一讲，主题为递推求解，涵盖了递推在解决数学问题和算法设计中的应用。" 在ACM程序设计中，递推是一种强大的工具，用于解决各种复杂问题，尤其是序列和图形分割等问题。递推求解通常涉及到从简单情况出发，通过构建递推关系来逐步推导出一般情况的解。 首先，我们看一个简单的例子，关于五个人年龄的问题。这个问题中，每个人都比前一个人年长2岁，第一个人说他10岁。通过递推，我们可以得出第n个人的年龄表达式为F(n) = 10 + (n - 1) * 2，这表明第n个人的年龄可以通过前一个人的年龄加上2来计算。简化后，公式变为F(n) = 10 + 2n - 2 = 2n + 8。 接下来，我们讨论了斐波那契数列，这是一个经典的递推序列，其定义为F(n) = F(n-1) + F(n-2)，初始值为F(0) = 0, F(1) = 1。斐波那契数列在许多算法和数学问题中都有应用。 在思考如何利用递推公式进行编程实现时，我们要注意不同方法的优缺点。例如，直接递归虽然直观，但可能会导致大量的重复计算，效率较低；而动态规划或记忆化搜索则能有效地避免重复计算，提高效率。 随后的题目涉及直线分割圆域的问题，我们发现递推公式F(n) = F(n-1) + n，进一步简化为F(n) = n(n+1)/2 + 1，这表明n条直线最多能把圆分割成特定的区域。 更复杂的问题如折线分割平面，需要更复杂的递推关系，如F(n) = F(n-1) + 4(n-1) + 1 或 Zn = 2n^2 - n + 1，这些都是通过深入分析问题并找出规模增加1时情况的变化来得出的。 总结递推求解的基本步骤包括： 1. 确定基础情况的解，即规模最小的情况下问题的解决方案。 2. 假设规模小一的情况已经解决，构建递推关系。 3. 分析规模扩大时的情况，找出所有可能的情形，并确保覆盖所有边界条件。 通过这种方法，可以解决各种递推问题，无论是简单的线性递推还是更复杂的二次甚至更高次的递推。递推求解在ACM竞赛和实际编程中都是一种重要的思维方式，它可以帮助我们构造高效算法，解决看似复杂的问题。