MATLAB数值积分实现：从一维到三维

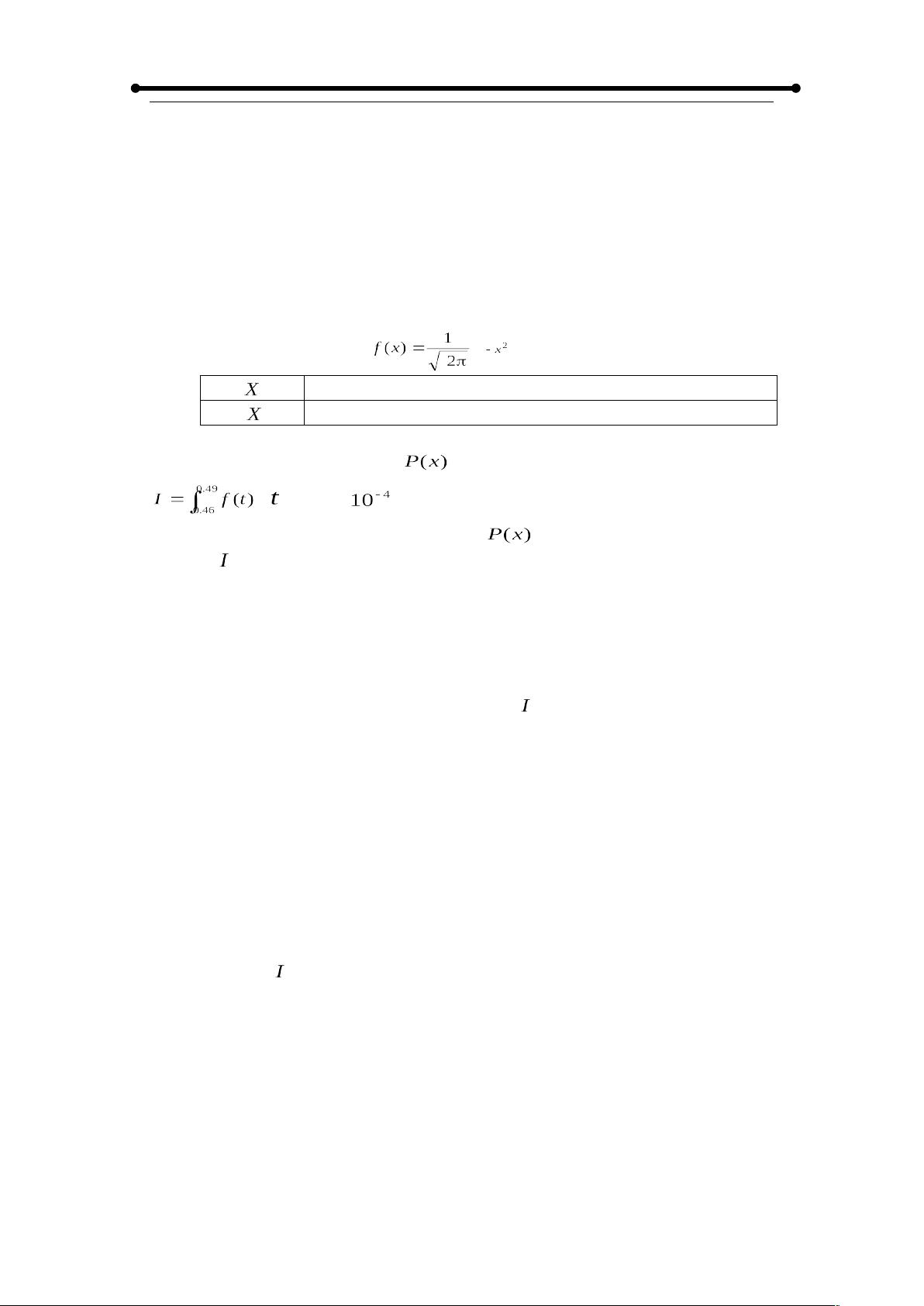
"该文档是关于使用MATLAB进行数值积分的教程，涵盖了从一维到三维的积分计算。文档详细介绍了如何使用MATLAB的符号计算功能进行定积分和变限积分，并展示了MATLAB程序示例。同时，还讨论了矩形公式在数值积分中的应用。" 在MATLAB中，数值积分是解决各种科学和工程问题的关键技术之一，它能够对不能解析求解的积分进行近似计算。本教程主要分为两个部分：符号计算和数值积分。 1. 符号计算： - 定积分：MATLAB的`syms`函数用于定义符号变量，`int`函数用于执行符号积分。例如，在案例中，计算由函数y=sin(x)和y=cos(x)在x=-0.5至x=1.5之间围成的区域面积，通过输入相应的MATLAB代码，可以得到精确的面积表达式和其浮点近似值。 - 变限积分：变限积分的MATLAB计算涉及对积分函数的微分。在给定的例子中，计算了函数的变限积分，并通过`diff`函数求得导数。 2. 数值积分的思想及其MATLAB程序： - 矩形公式：MATLAB提供了一个名为`sum`的函数来实现数值积分。它可以对序列求和，从而近似积分。例如，为了计算函数e^(sin(x))在区间[0, π/2]上的积分，使用矩形法将区间等分为20份，然后对每个小矩形的面积求和，与精确值进行比较。 在实际应用中，数值积分方法如矩形法、梯形法、辛普森法则等，可以根据问题的特性选择合适的算法。这些方法都是通过对积分区间进行分割，然后近似每个子区间的积分，最后将所有近似值相加来得到整个积分的近似值。 通过上述MATLAB代码示例，我们可以看到，MATLAB为数学计算提供了强大的工具，无论是对于简单的定积分，还是复杂的变限积分，或者是基于特定数值积分方法的编程实现，都提供了便捷的接口和函数支持。这使得科研人员和工程师能够快速准确地处理各种积分问题，而无需手动计算或依赖复杂的数学软件。