数控技术解析：步进电机与插补算法

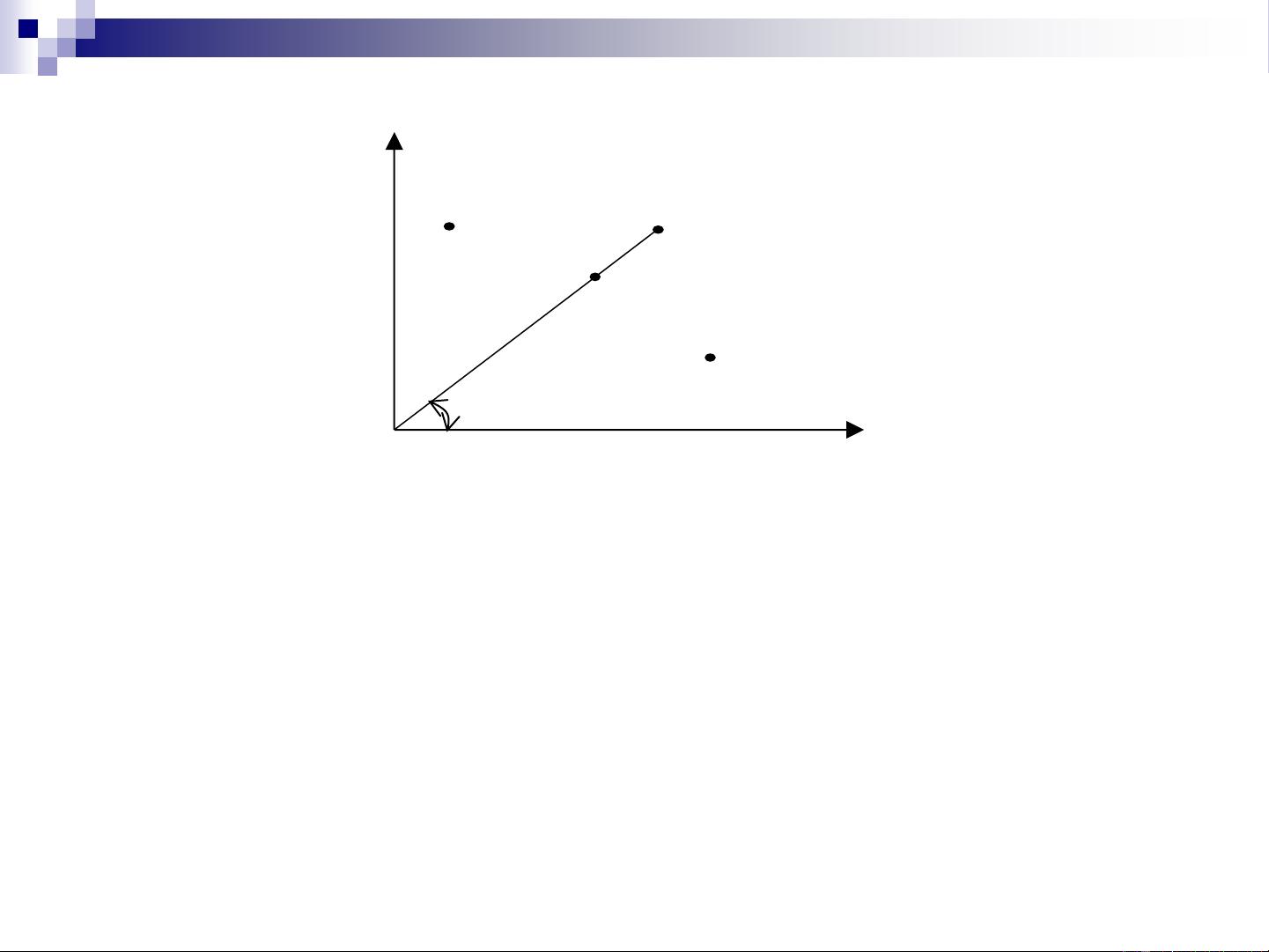
"电子-插补算法及步进电机.pdf" 这篇文档主要讲述了数字控制技术，特别是与单片机和嵌入式系统相关的STM32-F0/F1/F2系列的应用。文档聚焦于插补算法和步进电机在数字控制中的作用，这对于理解和实现精密机械运动控制至关重要。 首先，数字控制技术广泛应用于各种设备，如数控机床、线切割机等，它以高精度和高效能著称。数字控制的基础原理包括将曲线或路径分割成多个线段，然后通过插补算法来确定这些线段之间的中间点。例如，文档中提到了将曲线分为直线段和曲线段，并记录关键点的坐标。 插补是数字控制系统中的核心算法，它的任务是在已知起点和终点坐标的情况下，计算出一系列中间点，使得这些点连成的折线尽可能接近原始曲线。这种计算过程是为了使执行机构（如步进电机）能够按照特定的速度和精度沿着曲线移动。每一步进电机的步进动作都对应着坐标的一个微小变化，即脉冲当量，通常设置为固定值。 文档中以图5-2为例，展示了如何用折线逼近直线段，并计算了从起点到终点所需的总步数。在这个例子中，通过坐标增量值（以脉冲当量为单位）来表示步进电机在x和y方向上的移动距离。 数字控制方式有三种：点位控制、直线切削控制和轮廓切削控制。点位控制仅关注设备从一个位置准确移动到另一个位置，不关心移动过程中的路径；直线切削控制则涉及在两点间沿直线进行切削操作；而轮廓切削控制更复杂，它需要设备按照预设的轮廓轨迹进行运动，常用于复杂形状的加工。 在嵌入式系统中，如STM32系列的单片机，这些控制算法往往由微处理器执行，通过驱动步进电机或其他执行机构来实现精确的机械运动。STM32-F0/F1/F2是STM32家族的一部分，它们具有不同性能和功能，适用于各种数字控制系统的设计。 总结来说，这份文档深入介绍了数字控制的基本原理，特别是插补算法在步进电机控制中的应用，以及不同类型的数字控制方式。这对于理解和设计基于单片机的数控系统，尤其是涉及到高精度定位和路径规划的项目，提供了重要的理论基础和技术指导。