AR过程参数估计与噪声分析：LMS滤波器实验

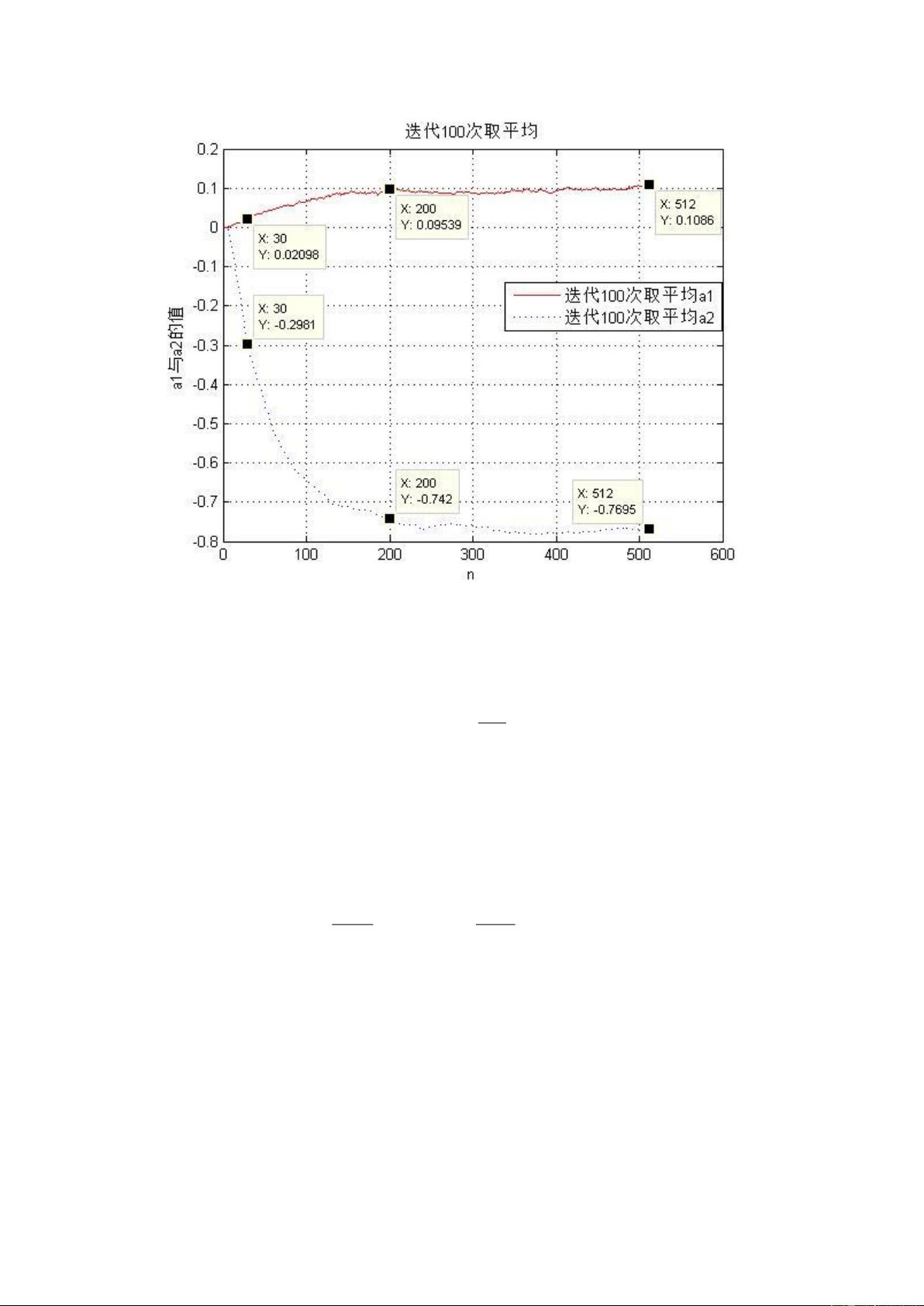
本篇文档是中科大DSPII计算机作业2的一部分，主要涉及数字信号处理（Digital Signal Processing，DSP）中的自回归（Autoregressive，AR）过程和最小均方误差（Least Mean Square，LMS）滤波器。主要内容包括： 1. **自回归过程**： - 提供了一个AR过程的差分方程模型，其中 \( x(n) \) 受到加性白噪声 \( v(n) \) 的影响，\( v(n) \) 的均值为0，方差为 \( \sigma^2_v \)。给定参数 \( a_1 = 0.1 \) 和 \( a_2 = -0.8 \)，要求计算 \( \sigma^2_v \) 使得 \( x(n) \) 的方差为1，这涉及到对AR过程稳态特性的理解。 2. **LMS滤波器估计AR参数**： - 使用长度为2的LMS滤波器来估计未知参数 \( a_1 \) 和 \( a_2 \)，步进大小 \( \delta = 0.05 \)。需要计算并绘制100个不同随机序列下滤波器参数 \( a_1 \) 和 \( a_2 \) 的平均值，以此得到滤波器的性能。 - 时间常数的实验结果将被比较理论值，展示了LMS算法在实际应用中的收敛性能。 3. **预测误差分析**： - 对于每个滤波器实例，计算预测误差 \( f(n) = x(n) - x_{n-1} \)，以及两个滤波器系数的误差 \( \epsilon_1(n) \) 和 \( \epsilon_2(n) \)。通过功率谱图展示 \( f(n) \) 如何表现出白噪声特性，而滤波器系数误差则应该随时间衰减，反映滤波器的稳定性和有效性。 这份作业着重考察了学生对AR模型的理解，LMS算法的实现，以及如何通过实验数据验证理论预测。它涵盖了数字信号处理的基本概念和技术，并要求学生具备数据处理、模拟和分析的能力。完成这类作业有助于提升对自回归模型和在线学习算法在实际问题中的运用能力。