运用多步决策方法解决商人安全渡河问题

"商人渡河模型的求解文档主要探讨了一个经典的数学模型问题，即商人安全渡河问题，该问题涉及到多步决策方法的应用。在复杂的社会经济环境中，多步决策模型有助于解决复杂的决策问题。文章通过运用多步决策方法构建了商人渡河的数学模型，并借助MATLAB软件进行了求解，最终得到了四种安全的渡河方案。问题背景是一个有三个商人和三个仆人的团队需要安全地利用只能载两人的船只渡河，仆人们计划在人数占优时背叛商人。模型建立过程中，将渡河过程视为一个状态与决策相互作用的动态过程，通过定义状态变量和决策变量，构建了一个类似迷宫的问题，目标是从初始状态安全地到达终止状态。模型求解部分描述了一个逐步的过程，包括参数设定、状态和决策的定义，以及利用算法寻找可行路径，以确保商人的安全。" 在这个模型中，关键知识点包括： 1. **多步决策模型**：这种模型适用于决策过程不能一次性完成，需要分步骤进行优化的情况。在商人渡河问题中，每个渡河步骤都是一个决策点，需要确保每个决策都符合安全条件。 2. **数学模型的建立**：问题被转换为状态空间模型，其中[u, v, 1/0]表示商人和仆人在两岸的分布以及船的位置。允许状态集合是满足安全条件的状态组合。 3. **决策变量**：决策变量[u, v]表示每次渡河时上船的商人和仆人数，决策变量集合包含了所有可能的组合，形成了一张决策网络。 4. **MATLAB软件应用**：MATLAB作为一种强大的数值计算和建模工具，被用来解决这个模型，寻找从初始状态到终止状态的安全路径。 5. **状态转移**：通过定义状态之间的转换规则，确保每次过渡都不会让仆人处于优势地位，从而确保安全。 6. **迷宫问题类比**：商人渡河问题被抽象为一个迷宫，每个决策变量对应迷宫中的一段路径，目标是找到从入口到出口的最安全路径。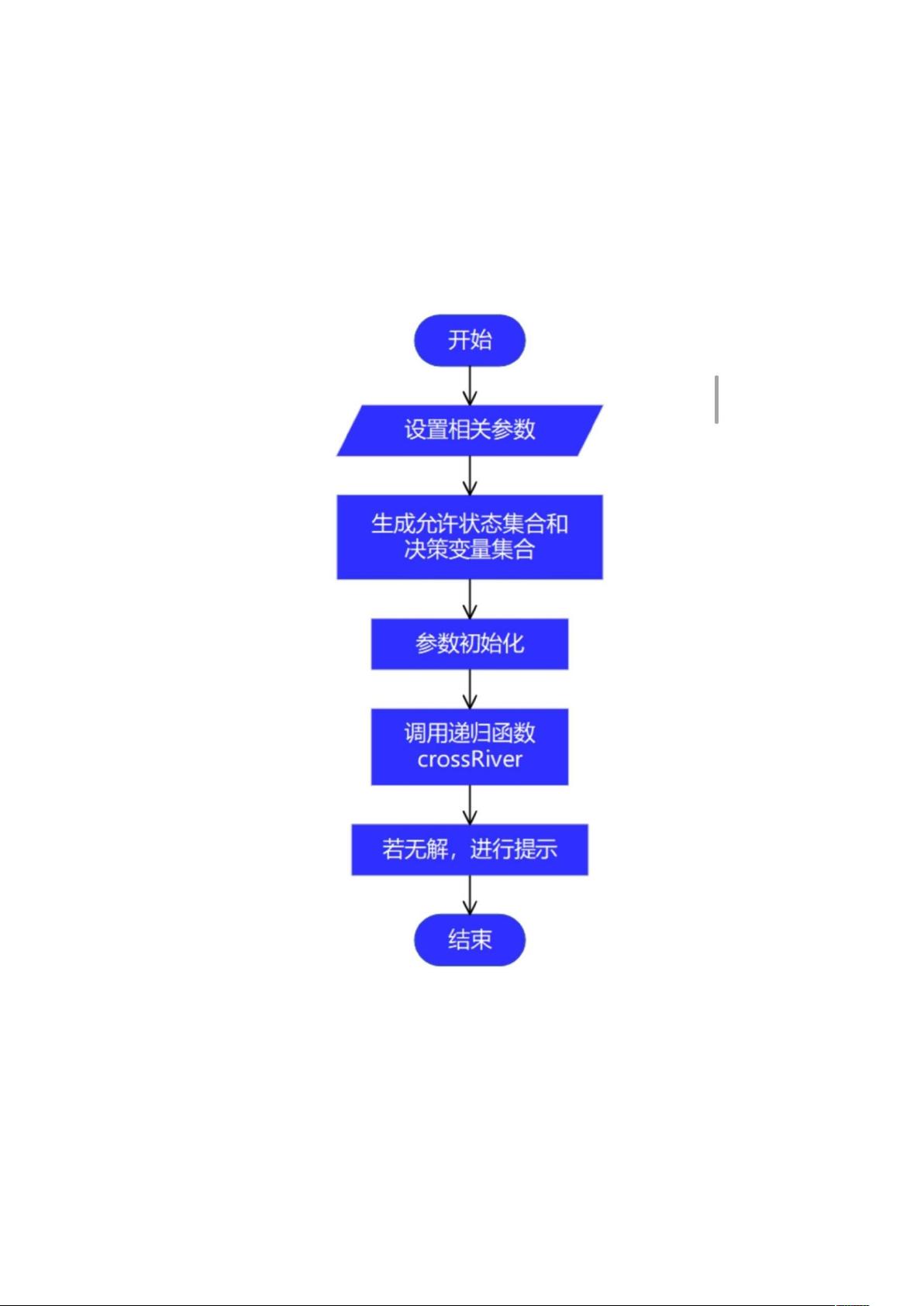 7. **模型求解流程**：包括设置参数、定义状态和决策、构建流程图，并可能涉及搜索算法（如深度优先搜索或广度优先搜索）来找到安全路径。 8. **安全渡河方案**：通过模型求解，找到了四种不同的渡河策略，这些方案满足了在任何时刻，商人数量不小于仆人的条件。 这个模型的解决不仅展示了数学在解决实际问题中的应用，也体现了逻辑思维和优化方法的重要性。通过这样的分析，我们可以学习如何将复杂问题简化并运用数学工具进行求解。