格与布尔代数：抽象代数的基石与计算机科学应用

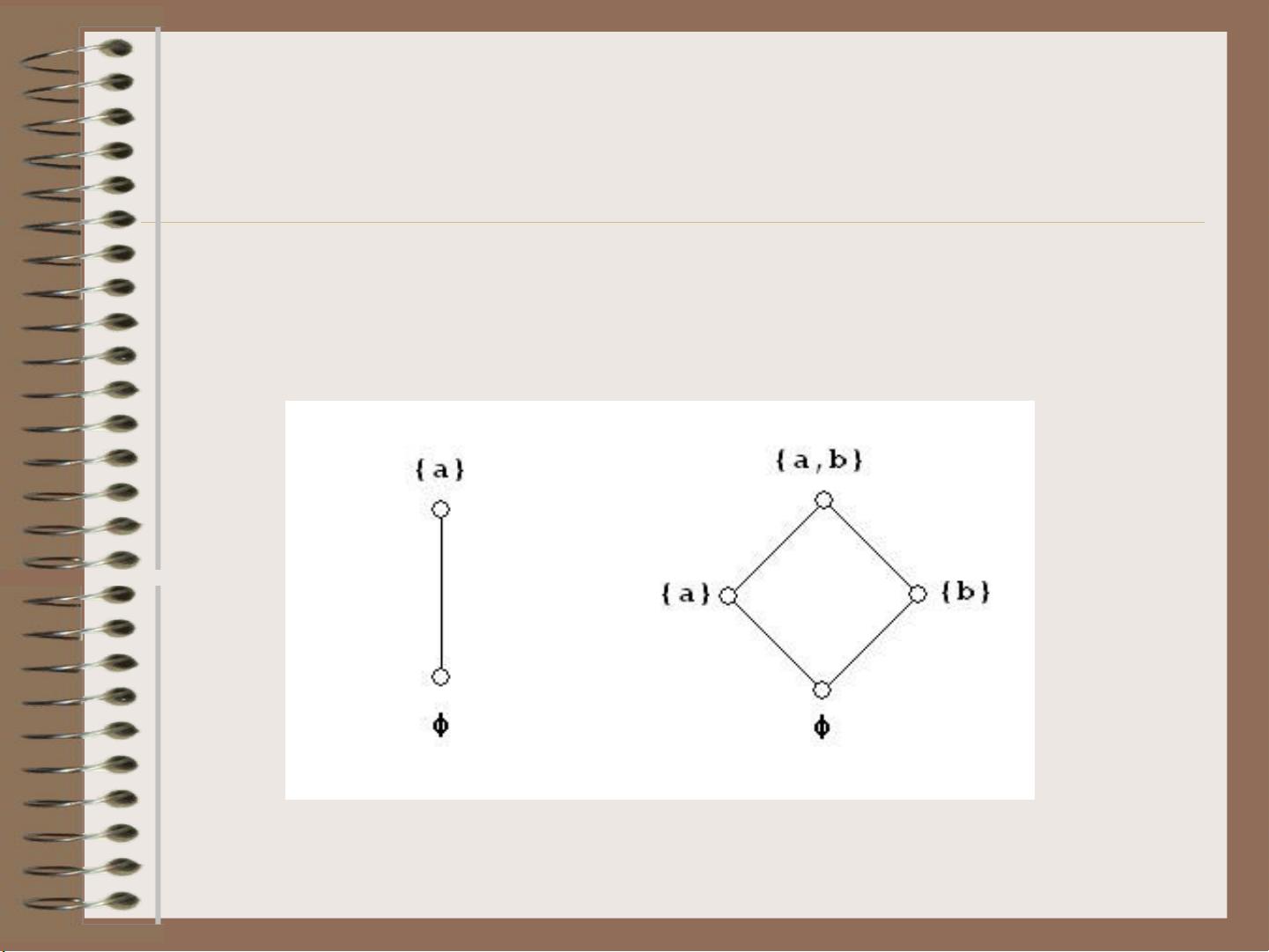
格与布尔代数是数学中的重要概念，它们源于对逻辑和集合论的深入研究，尤其在计算机科学中扮演着关键角色。格，最初在20世纪30-40年代发展起来，是一种偏序集合，其中任何非空有限子集都有上确界（并）和下确界（交），这些运算符满足一定的公理，如幂等、交换、结合、分配和吸收律。格可以看作是一个代数系统的基础，它是布尔代数的推广，后者是格的一种特殊情况，由英国数学家乔治·布尔在19世纪中叶创立。 在数学中，命题逻辑和集合论是格理论的基石。命题代数是逻辑运算（如AND、OR）构成的代数结构，其中的运算符满足幂等律等基本规则。而幂集代数则是基于集合操作（如并集和交集）的代数，同样遵循类似的定律，并且引入了补集和否定的概念，使得它们遵循德摩根定律。 布尔代数在此基础上进一步扩展，它不仅是一个有补分配格，即每个元素都有唯一的上界和下界，还要求这个偏序集合具有更强的代数特性。布尔代数在计算机科学中广泛应用，例如在有限自动机理论、开关网络分析以及逻辑设计中，它们提供了强大的工具来处理和理解复杂系统的逻辑结构。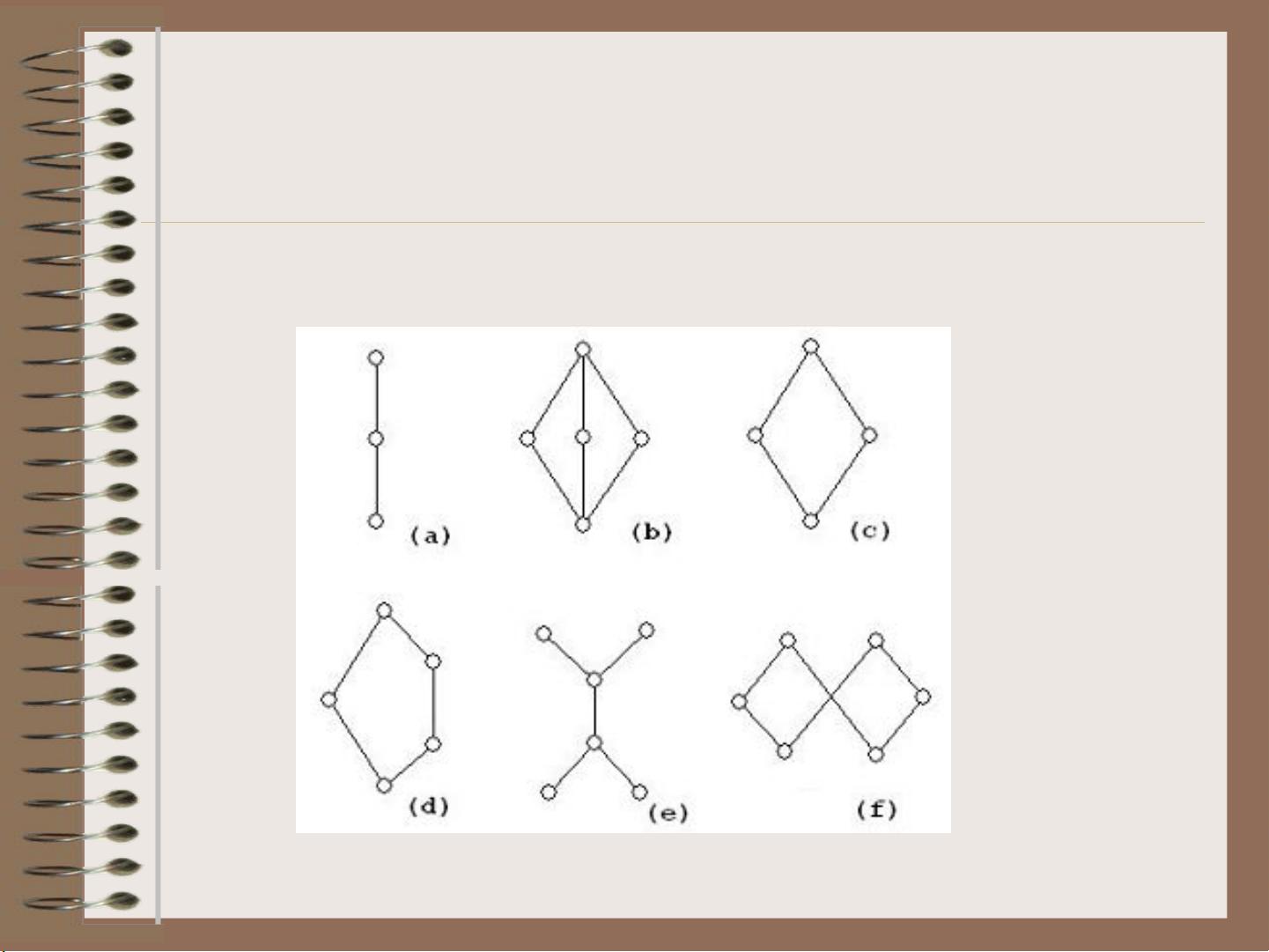 研究格和布尔代数时，首先要理解偏序和确界的性质，因为这是构建这两个代数体系的基础。在定义上，格的上确界和下确界被视为格内的二元运算，体现了它们在抽象代数中的核心地位。 格与布尔代数是数学逻辑和代数结构的重要组成部分，它们不仅连接了数学的多个领域，还在现代科技特别是计算机科学中发挥着不可替代的作用。理解这些概念，对于深入学习计算机科学、逻辑学以及相关工程学科至关重要。