程序驱动的分支预测技术

需积分: 9 174 浏览量更新于2024-08-01 收藏 151KB PDF 举报

"Branch Prediction For Free" 这篇论文探讨了如何在编译器中实现分支预测以提高程序性能，特别是关注于无需使用耗时的“编译-分析-再编译”周期的预测方法。传统的基于配置的分支预测器依赖于对程序运行的详细统计信息，这需要一个繁琐的过程。然而，作者提出了一种程序基础的分支预测器，它能够对C和Fortran编写的大量多样化的程序提供有效的预测。论文的核心在于利用自然循环分析来预测控制循环迭代的分支，并设计了一些简单的启发式策略来预测非循环分支，这些分支在许多程序的动态分支计数中占据主导地位。尽管这些启发式策略的分析复杂度低，但它们在覆盖率和错误率方面表现良好。作者指出，虽然程序基础的预测可能不如基于配置的预测准确，但其效果已经足够实用。此外，论文还讨论了如何通过利用编译器可获取的额外类型和语义信息来进一步改进这些启发式策略。这表明，如果能更深入地理解和利用程序的结构和上下文，分支预测的精度和效率可以得到提升。论文的作者是Thomas Ball和James R. Larus，他们都是计算机科学领域的专家，分别来自威斯康星大学麦迪逊分校的计算机科学系。这篇论文发表于1993年的ACM SIGPLAN '93 Conference on Programming Language Design and Implementation，强调了编译器在优化代码执行中的重要作用，特别是在处理分支决策时，这直接影响到现代处理器的流水线性能。 “Branch Prediction For Free”这篇论文揭示了如何在不增加额外开销的情况下，通过编译器内部的简单策略实现分支预测，从而提高程序执行速度，这对于理解和改进编译器优化技术具有重要意义。尽管它在准确性上可能无法完全替代基于配置的预测，但这种方法提供了一个实用且高效的替代方案，特别是在考虑到实际开发效率和资源限制时。

heuristics for non-loop branches and measures their effec-

tiveness in isolation. Section 5 considers combining these

simple heuristics into a complete heuristic and contains the

results for this heuristic. Section 6 presents results on how

our heuristic performs at ﬁnding sequences of instructions

without a mispredicted branch. We compare proﬁle-based

methods for measuring this quantity with trace-based

methods and show why trace-based methods are preferable.

Section 7 examines the performance of our heuristic on dif-

ferent datasets. Section 8 reviews related work and Section

9 concludes the paper.

2. BACKGROUND

We restrict our heuristics to predicting two-way conditional

branches with ﬁxed targets. Throughout the paper, the

word branch refers to such branches. We do not consider

branches whose target is dynamically determined (by

lookup in a jump table, for example). Associated with each

conditional branch instruction is its target successor—the

instruction to which control passes if the branch condition

evaluates to true—and its fall-thru successor—the instruc-

tion to which control passes if the branch condition evalu-

ates to false.

We used our proﬁling and tracing tool QPT [2] both as a

platform for studying branch behavior and for making

branch predictions. QPT takes as input a MIPS executable

ﬁle and produces an instrumented program that generates an

edge proﬁle (i.e., for each branch, a count of how many

times control passes to the target and fall-thru successor)

when run. QPT can also instrument a program to produce

an instruction and address trace. Since QPT operates on an

executable ﬁle, all program procedures are analyzed. The

numbers in this paper include DEC Ultrix 4.2 library pro-

cedures as well as application procedures.

In order to instrument an executable ﬁle, QPT builds a

control ﬂow graph for each procedure in the executable ﬁle.

Each vertex in the control ﬂow graph represents a basic

block of instructions. A basic block ending with a condi-

tional branch corresponds to a vertex in the control ﬂow

graph with two outgoing edges. The root vertex of the con-

trol ﬂow graph is the entry point of the procedure. A basic

block containing a return (procedure exit) has no successors

in the control ﬂow graph.

Some of our heuristics make use of the control ﬂow

graph’s domination and postdomination relations [1]. A

vertex v dominates w if every path from the entry point of

the procedure to w includes v. A vertex w postdominates v

if every path from v to any exit vertex includes w. If the

successor of a branch postdominates the branch, then no

matter which direction the branch takes, the successor even-

tually executes.

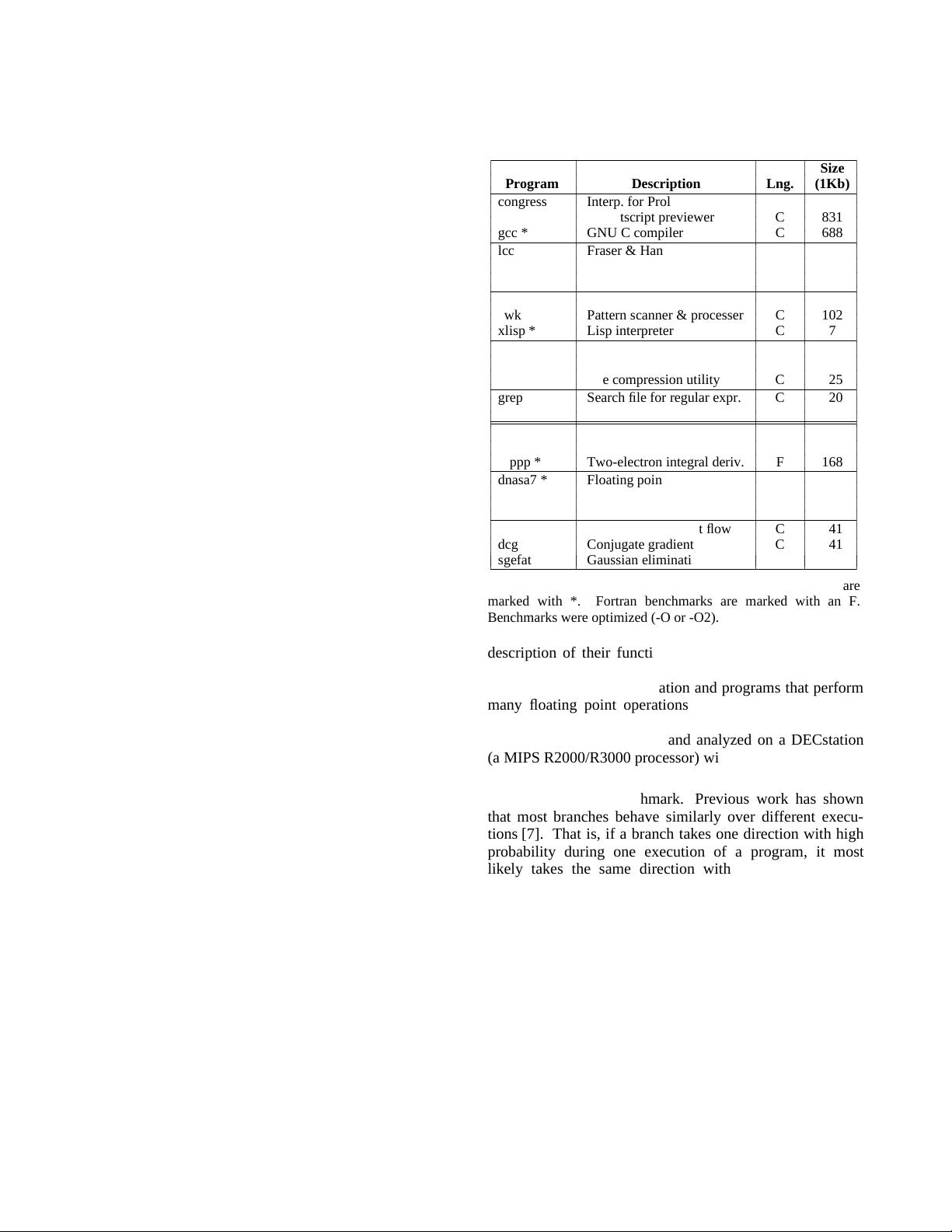
We analyzed the programs in the SPEC89 benchmark

suite [4], along with a number of other programs. These

benchmarks (23 of them) are listed in Table 1, along with a