NOIP图论：最短路算法详解与Floyd方法

"NOIP图论最短路.pptx"文件主要讲述了图论中的经典问题——最短路径算法，特别是在C++编程语言中的实现。该内容涵盖了以下几个关键知识点： 1. 问题背景： 最短路径问题是图论中的核心问题，目的是找出图中两个节点之间的最短连接路径。这在实际应用中非常常见，如在网络路由、地图导航等场景中。 2. 算法概述： - Floyd算法：Floyd算法（通常称为Floyd-Warshall算法）是一种动态规划方法，用于求解任意两点之间的最短路径。它通过迭代地更新图中所有节点对之间的距离，直到找到全局最优解。其时间复杂度为O(N^3)，适用于存在负边权的图。 - 算法步骤： a. 初始化：对于每个节点对(u, v)，根据它们之间是否有边以及边的权重设置初始距离。如果无边，距离设为无穷大。 b. 使用三层嵌套循环，分别对应k、i和j，其中k作为中间节点，更新每对节点之间的距离，如果通过k可以得到更短路径，则更新距离。 c. 循环结束后，dis[i][j]即为起点i到终点j的最短路径。 3. 路径记录： 输出最短路径时，除了距离外，还需要记录路径，通常通过前驱节点(pre[])来实现。每次更新距离时，如果发现新的最短路径，会更新前驱节点，以便后续重构路径。 4. 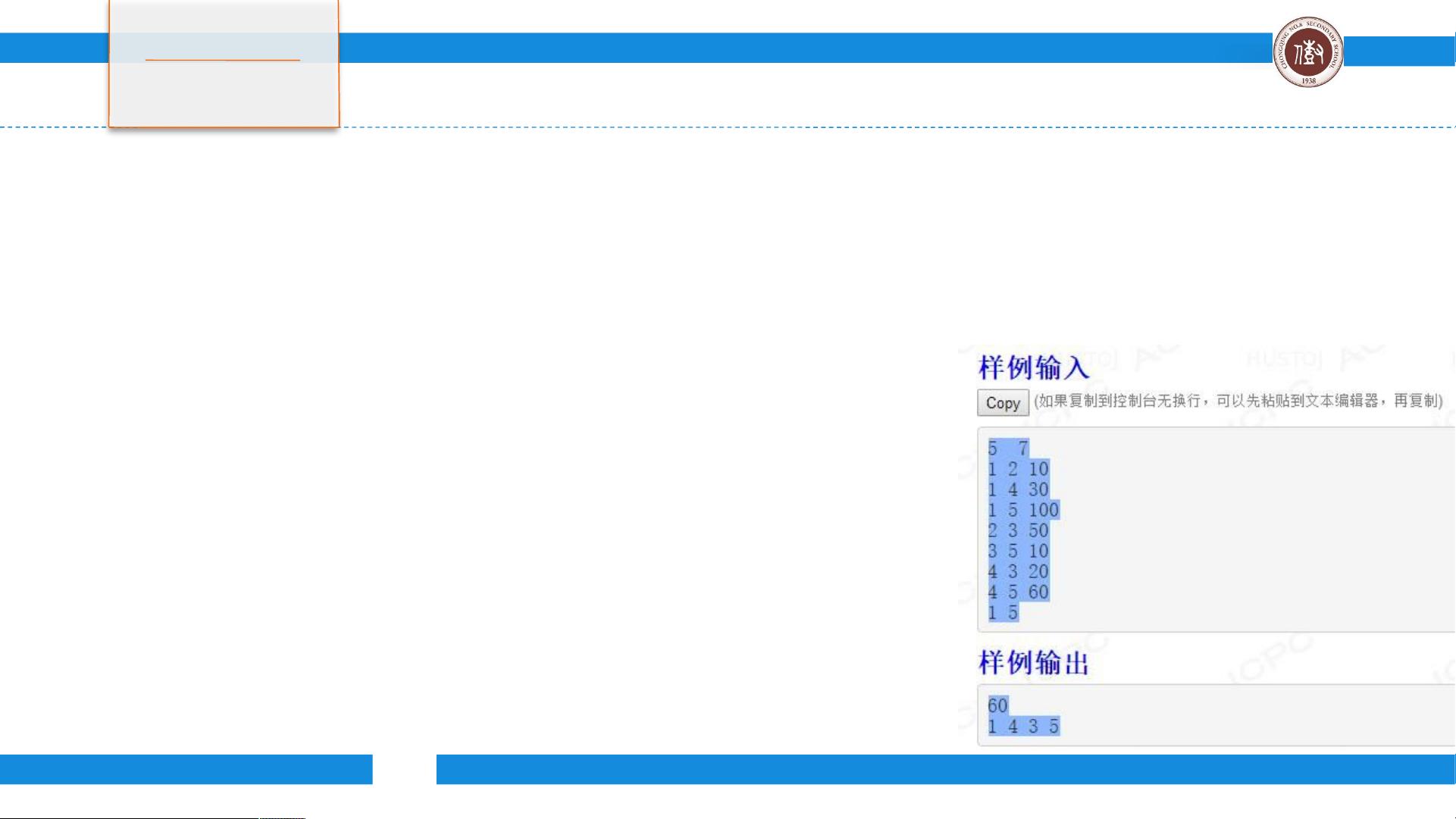实际应用： - BZOJ8171问题：解决一个无向图中，从起点S到终点E的最短路权值和问题，利用Floyd算法求解，限制了节点数量N（不超过100），且坐标范围较大(-10000~10000)。 5. 疑问解答： 关于算法中为何将中间点的枚举循环k放在最外层，这是因为Floyd算法的目的是通过比较一定不经过k点与一定经过k点的不同路径，来不断优化整体的最短路径估计。 总结来说，这份PPT详细讲解了如何用C++实现Floyd算法来解决最短路径问题，包括算法的原理、步骤、数据结构的使用，以及如何将其应用于特定的实例。这对于理解和解决实际的图论问题具有很高的价值。