C++内排序算法详解:快速排序与插入排序
99 浏览量
更新于2024-07-15
收藏 730KB PDF 举报
C++中的八大排序算法是内部排序的重要组成部分,主要针对的是内存中的数据排序,而非涉及大规模外存操作的外部排序。这些排序算法通常被分为两类:时间复杂度较高的O(n^2)算法,如直接插入排序,以及更高效的O(nlog2n)算法,如快速排序、堆排序和归并排序。
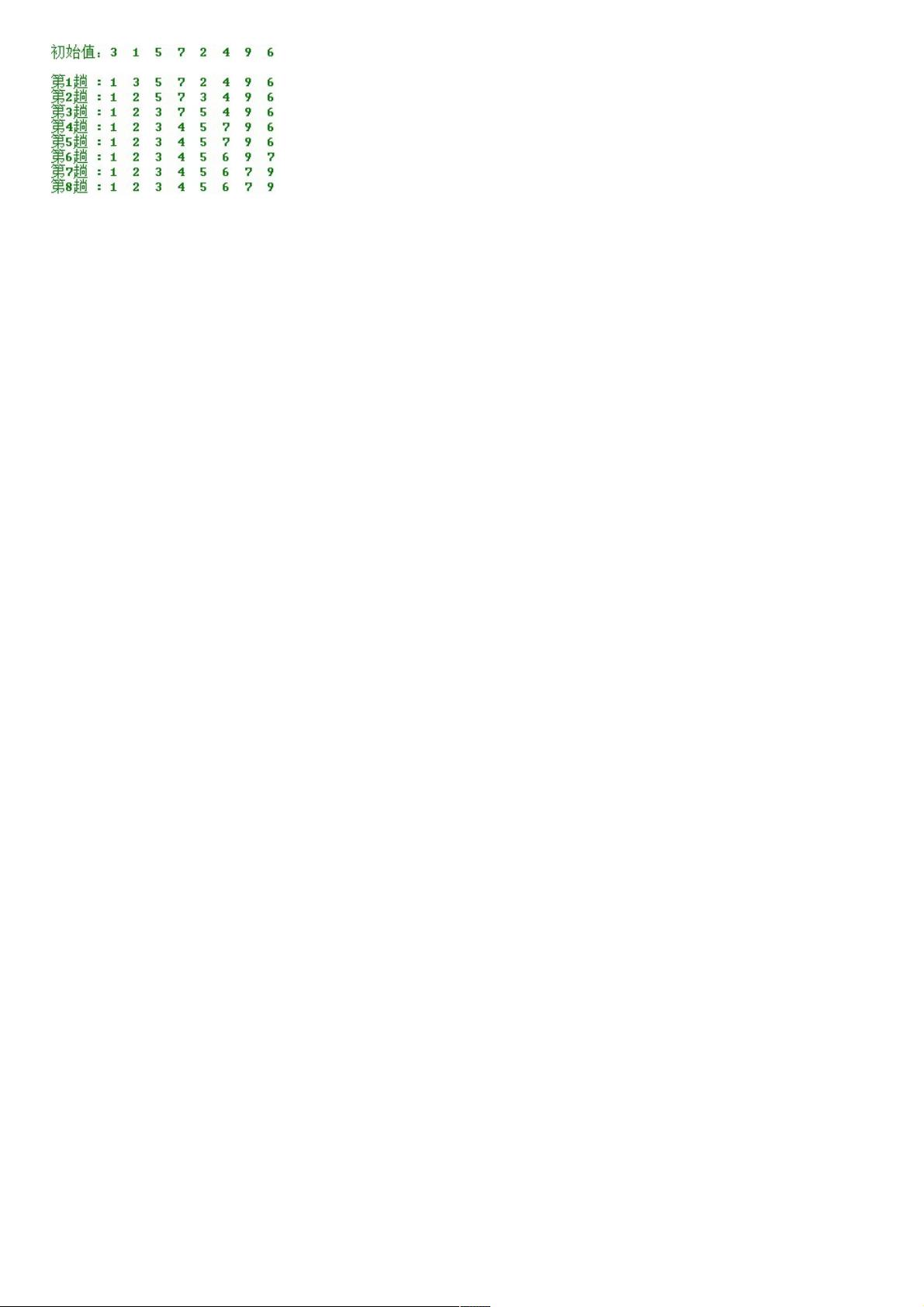
1. **直接插入排序 (Straight Insertion Sort)**:
- 基本思想是将每个元素依次与前面已排序的元素进行比较,找到合适的位置插入,保持有序状态。
- 插入排序的核心在于设立哨兵,避免处理边界情况。例如,在`InsertSort`函数中,通过`a[i] = a[i-1]`的操作,将待排序元素与已排序部分进行交换,然后通过`while`循环找到正确的位置。
- 插入排序的稳定性使其在某些场景下具有优势,比如数据中存在大量重复元素时,因为相等元素的顺序不会改变,插入排序可以保持原有的相对位置。
- 时间复杂度:最坏情况下是O(n^2),但实际性能受初始序列的影响,比如接近有序序列时,效率会提高到接近线性。
2. **希尔排序 (Shell's Sort)**:
- 希尔排序是插入排序的一种优化版本,通过设定一系列增量序列,将数据分组进行插入排序,逐渐缩小增量直到1,最后达到完全排序。
- 相比直接插入排序,希尔排序在一定程度上减少了比较次数,提高了效率,尤其在数据量大且部分有序的情况下。
- 希尔排序的时间复杂度一般介于O(n)和O(n^2)之间,具体取决于增量序列的选择。
3. **快速排序 (Quick Sort)**:
- 快速排序是基于分治策略的高效排序方法,选择一个基准值,将数组分为两部分,一部分所有元素都小于基准,另一部分所有元素都大于基准,然后递归地对这两部分进行排序。
- 平均时间复杂度为O(nlog2n),但最坏情况下可能退化到O(n^2),不过这种情况较少见,通常通过随机化选取基准来避免。
- 快速排序是不稳定的排序算法,但可以通过一些技巧实现稳定性,如三向切分快速排序。
4. **堆排序 (Heap Sort)**:
- 堆排序利用了二叉堆数据结构,首先将待排序数组构建成最大堆或最小堆,然后每次取出堆顶元素(最大或最小),重构堆,直到堆为空。
- 时间复杂度始终为O(nlog2n),且空间复杂度较低,适合数据量大且内存有限的情况。
5. **归并排序 (Merge Sort)**:
- 归并排序也是分治策略,将数组一分为二,分别排序,然后合并。这个过程递归进行,直到子数组只剩下一个元素。
- 时间复杂度稳定为O(nlog2n),但需要额外的空间来存储临时数组,适用于对内存空间限制不敏感的场景。
C++中的八大排序算法各有特点,选择哪种取决于数据规模、数据特性、内存可用性以及对排序稳定性的需求。在实际应用中,根据具体情况评估每种算法的效率,以便作出最优决策。
714 浏览量
294 浏览量
164 浏览量
294 浏览量
weixin_38599545
- 粉丝: 7
最新资源
- 深入解析ARM嵌入式Linux系统开发教程
- 精通JavaScript实例应用
- sndspec: 将声音文件转换为频谱图的工具
- 全技术栈蓝黄企业站模板(HTML源码+使用指南)
- OCaml实现蒙特卡罗模拟投资组合运行于网络工作者
- 实现TMS320F28069 LCD显示与可调PWM频率输出
- 《自动控制原理第三版》孙炳达课后答案解析
- 深入学习RHEL6下KVM虚拟化技术
- 基于混沌序列的Matlab数字图像加密技术详解
- NumMath开源软件:图形化数值计算与结果可视化
- 绿色大气个人摄影相册网站模板源码下载
- OpenOffice集成jar包:实现Word与PDF转换功能
- 雷达数字下变频MATLAB仿真技术研究
- PHP面向对象开发核心关键字深入解析
- Node.js中PostgreSQL咨询锁的实践与应用场景
- AIHelp WEB SDK代码示例及集成指南