N=4超杨米尔斯理论：能量-能量相关性的新公式与计算

24 浏览量更新于2024-09-02 收藏 312KB PDF 举报

"这篇研究论文深入探讨了N = 4超级杨-米尔斯理论（N = 4 sYM）中的能量-能量相关关系（EEC），并提出了一种新的方法，可以直接从有限相关函数中计算EEC，从而规避红外发散问题。作者包括J.M. Henn, E. Sokatchev, K. Yan和A. Zhiboedov，分别来自德国马克斯-普朗克物理研究所、法国安纳西-蒙布朗什大学和瑞士欧洲核子研究中心。文章于2019年4月收到，并在同年8月发表。" 在N = 4超级杨-米尔斯理论这一高度对称的量子场论中，能量-能量相关关系是一个关键的物理量，它描述了系统中不同能量态之间的关联。传统的计算方法往往会在处理红外发散时遇到困难，而这项研究则提出了一种创新的计算策略，直接从有限相关函数出发，有效地解决了这一问题。这种方法的新颖之处在于，它将EEC与四点相关函数的三重间断直接联系起来，简化了计算过程。在N = 4 sYM的微扰理论框架下，研究人员利用这个新公式计算了EEC的次领先阶（next-to-next-to-leading order）。他们得到了一个可以通过数值方法直接求解的双积分表达式。值得注意的是，某些积分核与日出图的费曼积分类似，这些积分可以被解析为椭圆函数，这是数学上复杂但有严格解的形式。此外，研究者还利用新公式对EEC进行了扩展，涵盖了背对背和共线这两种极限情况。这不仅增加了理论预测的精确度，也为实验上的观测提供了理论依据。背对背和共线范围的分析对于理解高能物理中的粒子分布和碰撞过程至关重要。这项工作深化了我们对N = 4超级杨-米尔斯理论的理解，特别是在处理复杂相关函数和红外问题方面的技术进步。这些成果不仅对理论物理学家，也对实验物理学家有着重要的指导意义，有助于推进高能物理领域的研究。通过开放获取的标签，这篇论文的成果可以被全球的研究者自由访问和应用，促进了科学知识的传播和交流。

Energy-energy correlation in N = 4 super Yang-Mills theory at

next-to-next-to-leading order

J. M. Henn,

E. Sokatchev,

K. Yan,

and A. Zhiboedov

Max-Planck-Institut für Physik, Werner-Heisenberg-Institut, 80805 München, Germany

LAPTh, Universit´e Savoie Mont Blanc, CNRS, B.P. 110, F-74941 Annecy-le-Vieux, France

Theoretical Physics Department, CERN, 1211 Geneva 23, Switzerland

(Received 3 April 2019; published 26 August 2019)

We develop further an approach to computing energy-energy correlations (EEC) directly from finite

correlation functions. In this way, one completely avoids infrared divergences. In maximally super-

symmetric Yang-Mills theory (N ¼ 4 sYM), we derive a new, extremely simple formula relating the EEC to

a triple discontinuity of a four-point correlation function. We use this formula to compute the EEC in N ¼ 4

sYM at next-to-next-to-leading order in perturbation theory. Our result is given by a twofold integral

representation that is straightforwardly evaluated numerically. We find that some of the integration kernels

are equivalent to those appearing in sunrise Feynman integrals, which evaluate to elliptic functions. Finally,

we use the new formula to provide the expansion of the EEC in the back-to-back and collinear limits.

DOI: 10.1103/PhysRevD.100.036010

I. INTRODUCTION

The energy-energy correlation (EEC) [1] measures the

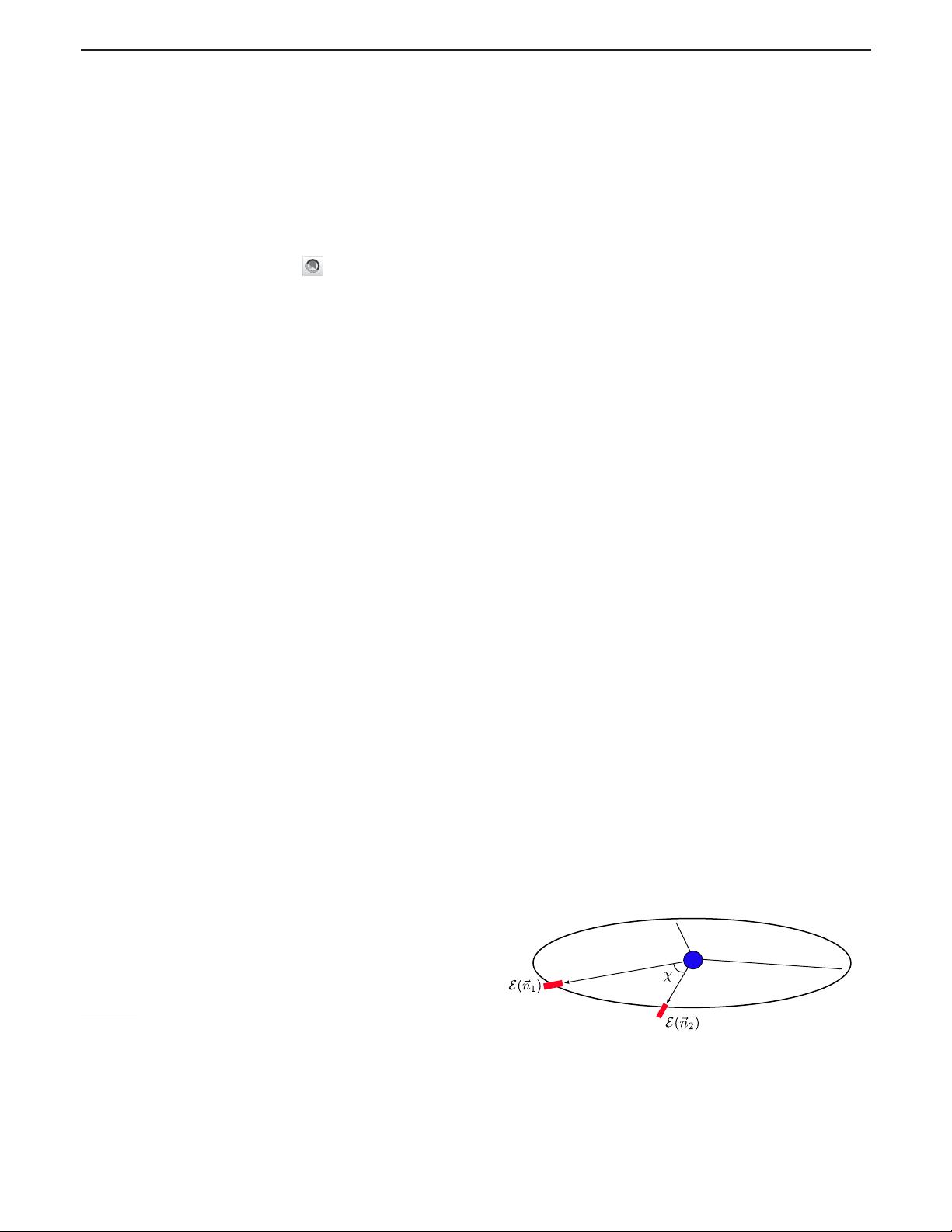
energy flow through a pair of detectors separated by an

angle χ; see Fig. 1. The EEC has several nice properties and

may help to understand better the nature of jets in quantum

field theory. It is an infrared-safe observable [2,3] that

can be computed perturbatively. Moreover, it has simple

factorization properties in the back-to-back (χ → π) [4–8]

and collinear (χ → 0) [9,10] limit. This knowledge can be

used to match fixed-order predictions to resummation

calculations [6–8]. On the other hand, the EEC is exper-

imentally measurable, and in particular has been used for

precision tests of QCD and measurement of the strong

coupling constant α

[11–13].

The EEC at leading order (LO) is known since [1], while

the next-to-leading order (NLO) and next-to-next-to-lead-

ing order (NNLO) results were obtained numerically in

Refs. [14–21] and [22,23], respectively. Only very recently,

the NLO result was computed analytically [24]. Analytic

results are important both conceptually and practically, for

example to test numerical codes and to control numerical

instabilities in special kinematic regions.

Although the EEC is infrared finite, the standard

approach to computing involves infrared divergent scatter-

ing amplitudes and phase-space integrals [24,25]. On the

other hand, it can be defined starting from correlation

functions, which are infrared finite [26 –30]. For example,

for e

þ e

−

→ γ



→ X, the main ingredient is a four-point

correlation function of two energy-momentum tensors

(representing the two detectors), and two electromagnetic

currents, which create the electron-positron pair from the

vacuum.

To the best of our knowledge, this approach has not yet

been implemented in QCD. On the other hand, these ideas

were applied in N ¼ 4 super Yang-Mills (sYM) [30–32],

culminating in the first analytic calculation of and EEC at

NLO [33]. The structure of this result, and in particular the

types of polylogarithmic functions appearing in it, foreshad-

o wed the structures later found in QCD [24]. Therefore, any

analytic information at NNLO is very desirable.

We show that for an analog of the electromagnetic

current in N ¼ 4 sYM, the EEC is computed by a new,

extremely simple formula, given by a twofold integral of a

particular triple discontinuity of the four-point correlation

function; see Eq. (7) below.

FIG. 1. Graphical representation of the energy-energy correla-

tion: particles produced out of the vacuum by the source are

captured by the two detectors located at spatial infinity in the

directions of the unit vectors



and



Published by the American Physical Society under the terms of

the Creative Commons Attribution 4.0 International license.

Further distribution of this work must maintain attribution to

the author(s) and the published article’s title, journal citation,

and DOI. Funded by SCOAP

PHYSICAL REVIEW D 100, 036010 (2019)

2470-0010=2019=100(3)=036010(7) 036010-1 Published by the American Physical Society

下载后可阅读完整内容，剩余6页未读，立即下载

weixin_38703823

粉丝: 6
资源: 939

N=4超杨米尔斯理论：能量-能量相关性的新公式与计算

强γ变形的N $$ \ mathcal {N} $$ = 4 SYM理论的全息对偶：导数，泛化，可积性和离散重新参数化对称性

N=4超杨-米尔斯理论的Yang-Baxter算符与散射振幅

N=4超杨米尔斯理论中半BPS算符的事件形状分析

圆上超级杨米尔斯的局部和非均匀热态

四维超杨米尔斯理论中的新型非摄动标度与胶球绑定能量

三维超杨-米尔斯理论与可压缩夸克物质的重力对偶研究

库仑分支上的强耦合N = 4超对称Yang-Mills等离子体。 一，热力学

相关函数的N = 4个超共形Ward身份

N = 1 $$ \ mathcal {N} = 1 $$时的有效动作，D5超对称规范理论：谐波超空间方法

量具耦合场，电流，异常和N = 1个超阳密斯有效动作

最新资源

库仑分支上的强耦合N = 4超对称Yang-Mills等离子体。一，热力学