随机信号分析：课程概览与随机变量基础

“投掷骰子出现点-第一讲：课程概述与随机变量基础” 课程“投掷骰子出现点”是一门深入探讨随机变量及其在实际应用中的基础课程。课程内容涉及概率论与数理统计的基本概念，尤其关注随机事件和样本空间的定义。在描述中，提到了两个具体的实例：投掷骰子出现1点和出现偶数点。这两种情况都是随机事件的例子，它们定义了特定的样本空间。样本空间是所有可能结果的集合，在骰子的例子中，样本空间是{1, 2, 3, 4, 5, 6}。 随机变量是概率论中的核心概念，它是一个函数，将样本空间的每个元素映射到实数线上的一点。在投掷骰子的例子中，可以定义两个随机变量：X表示出现的点数，Y表示是否出现偶数点。X的值域是{1, 2, 3, 4, 5, 6}，而Y的值域是{0, 1}，其中0代表出现奇数点，1代表出现偶数点。 课程的讲师是罗鹏飞教授，提供了联系方式以便学生咨询。课程内容不仅限于随机变量的基础知识，还涵盖了随机信号分析与处理的广泛领域。课程的发展历程反映了统计无线电理论和信号检测与估计等主题随着时间的推移而逐渐演变，最终形成了现代随机信号分析与处理这门课程。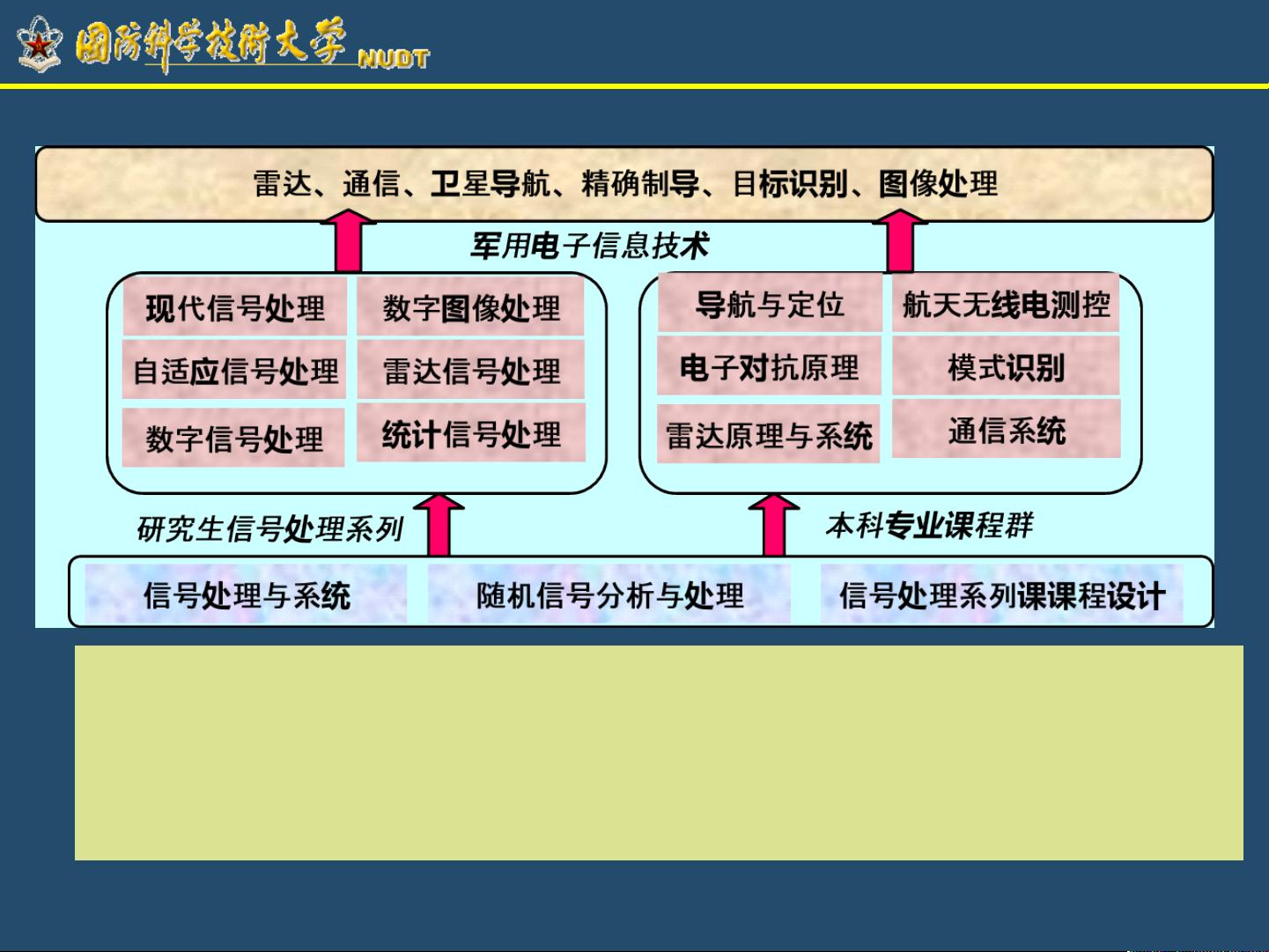 课程的重要性在于，随机信号广泛存在于我们的日常生活和各个科学领域中，如语音波形、通信信号、生物信号、地震信号、温度记录等。由于这些信号无法用解析表达式或确定性方式建模，因此理解和处理随机信号对于电气工程和计算机科学至关重要，特别是在通信、雷达、导航、计算机视觉和数字信号处理等领域。 课程的学习目标可能包括理解随机过程的基本性质，掌握随机变量的分布和统计特性，以及学会如何分析和处理实际世界中的随机信号。教学内容会涵盖随机变量的概率分布、期望值、方差等统计参数，以及如何利用这些知识进行信号检测和估计。 教学组织和安排可能包括理论讲解、实例分析、实验练习和项目设计，旨在培养学生的理论素养和实践能力。学习策略可能强调理论与实践相结合，鼓励学生积极参与讨论，通过解决问题来深化对随机变量和随机信号的理解。 这门课程是理解并应对现实世界中复杂、不确定现象的关键，通过学习，学生将能够运用随机变量理论解决实际问题，例如在通信系统中进行有效的信号处理和决策制定。