C语言实现矩阵LU分解及其逆运算实例

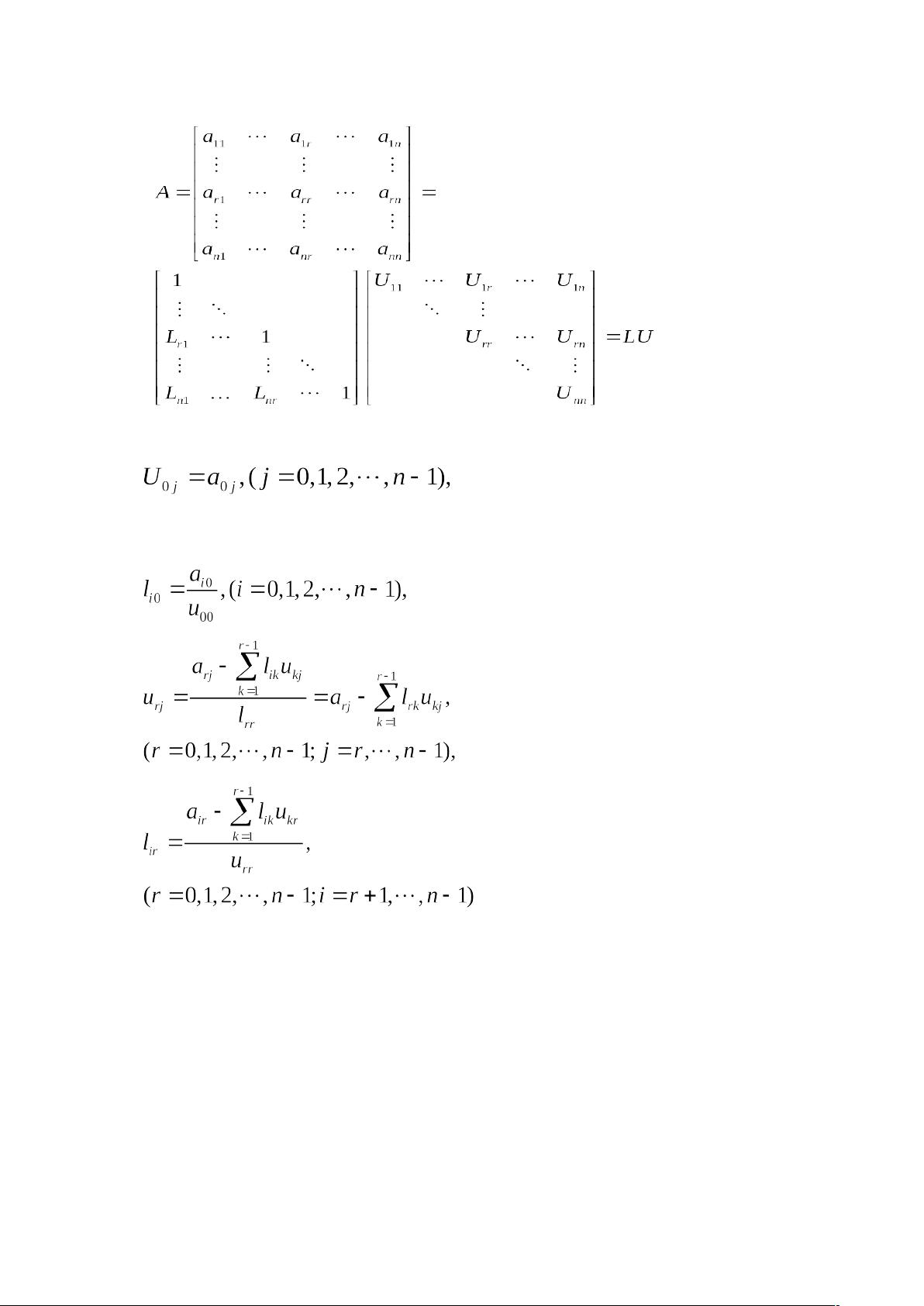
矩阵的LU分解是一种重要的线性代数工具，它在数值计算和解决线性系统中扮演着核心角色。LU分解的基本思想是将一个n阶方阵A分解为一个下三角矩阵L（对角线元素为1）和一个上三角矩阵U的乘积，即A = LU。这种分解的前提条件是矩阵A的各阶顺序主子式非零，确保了分解的存在性和唯一性。 1. 矩阵LU分解的迭代过程 - LU分解遵循特定的规则：从第一行开始，逐行确定U矩阵的元素，然后根据已知的U和L的部分，更新剩余行的值。这个过程持续到所有行都处理完毕，形成U矩阵。接着，从第一列开始，逐列确定L矩阵的元素，同样基于U和先前确定的L部分。这样，L矩阵在U矩阵之后一个节点完成。 2. L矩阵和U矩阵的求逆 - 对于下三角矩阵L，其逆矩阵R可以通过递推公式计算，如公式（8）所示。上三角矩阵U的逆则可以用类似的方法得到，公式（9）给出了具体的计算方式。 - 矩阵求逆是一个迭代过程，涉及多次计算，U矩阵的逆按行顺序进行，而L矩阵的逆按列顺序进行，两者交替进行，直到得到整个逆矩阵。 3. 矩阵相乘与逆矩阵的计算 - 最终，通过将U矩阵的逆u与L矩阵的逆R相乘，得到原矩阵A的逆矩阵A^-1，这一步是整个求逆操作的核心步骤，用公式（10）表示。 4. 实例演示 - 如题中所给的例子，对4阶矩阵进行LU分解，首先将矩阵分解为L和U，然后分别求这两个矩阵的逆，最后通过矩阵相乘得到原矩阵的逆。例如，给定矩阵A和初始的分解，通过计算逐步确定L和U的元素，并根据公式（4）-（7）进行迭代，最终得到L和U的完整形式以及它们的逆矩阵。 矩阵的LU分解在编程实践中常用于解决线性方程组、求矩阵特征值等问题，由于其高效性和稳定性，被广泛应用于科学计算和工程应用中。C语言编程实验通常会要求学生实际编写代码实现上述算法，以加深理解和掌握这一关键的数学工具。