数理逻辑与一阶逻辑复习：命题符号化、推理规则与等值演算

"第一二四部分 复习提纲（离数）.pptx" 这篇复习提纲涵盖了数理逻辑的重要概念，特别是命题逻辑和一阶逻辑。在命题逻辑部分，主要考点包括： 1. 命题和真值：理解简单的命题、命题联结词（非、与、或、蕴含、双蕴含）以及如何将日常语言中的命题符号化。例如，"除非我很累，否则我就去学习" 可以符号化为 `┐PQ` 或 `Q∨┐P`。 2. 命题公式的真值表和等值演算：涉及不同联结词的优先级，如括号最高，然后是非、与、或、蕴含、双蕴含。此外，还有24个基本的等值式，用于简化命题公式。 3. 判断公式类型：识别重言式（总是为真的命题）、矛盾式（总是为假的命题）和可满足式（至少存在一种情况使得公式为真）。 4. 极大项、极小项的概念，以及主析取范式和主合取范式之间的关系。例如，重言式和矛盾式的例子分别给出了7组不同的组合，除了101之外的所有组合都表示重言式，而M0ΛM1ΛM3等价于一个主合取范式。 5. 推理规则和自然推理系统的应用：通过实例展示了如何构建推理证明，例如根据给定的条件来决定科研人员的出国进修选派。 在一阶逻辑部分，重点讨论了： 1. 符号化的命题：如"金子是闪光的，但闪光的不一定是金子"，可以用量词来表达为 `∀x(R(x)→Q(x))ΛØ∀x(Q(x)→R(x)))`。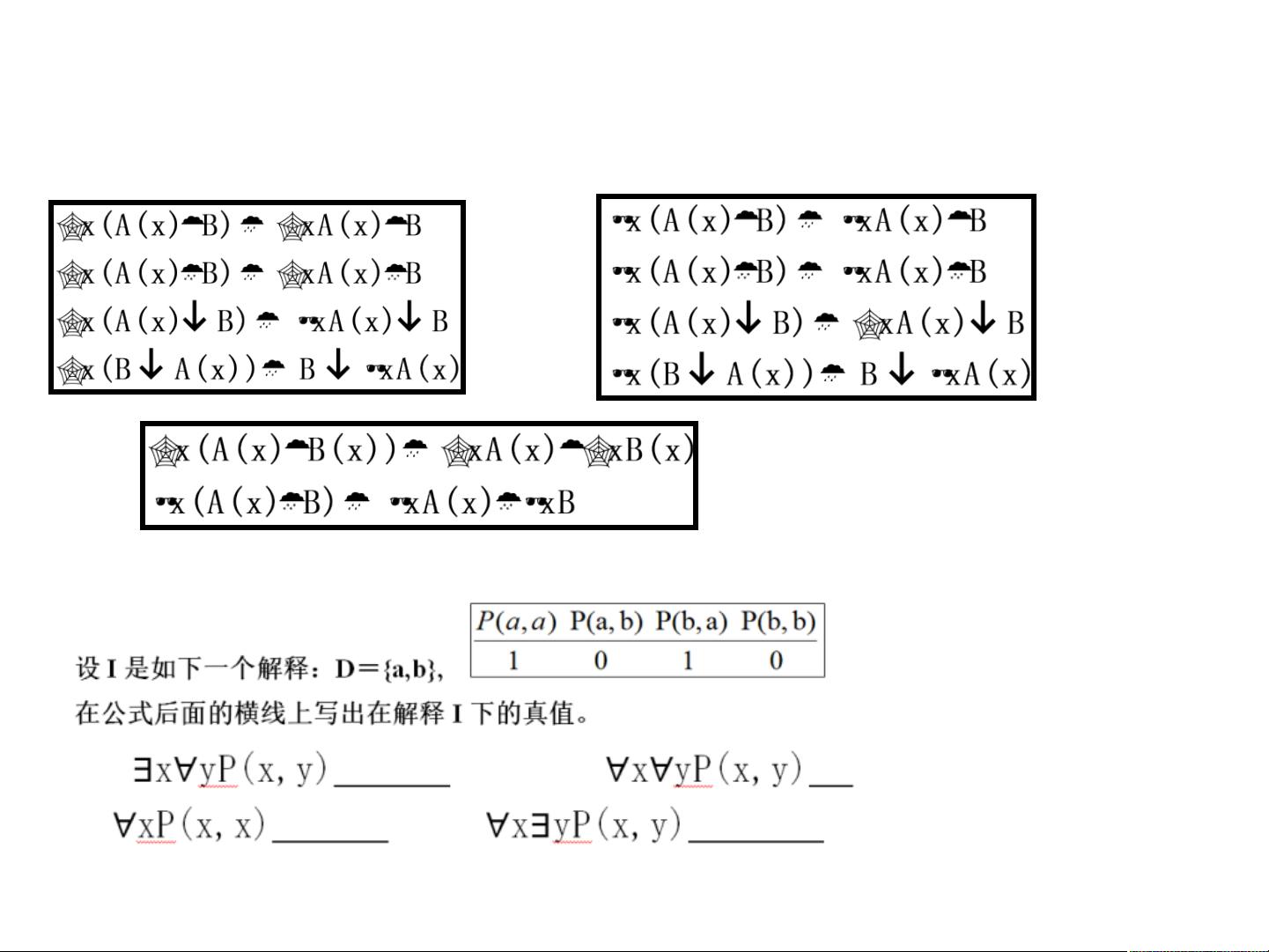 2. 重要的等值式，如量词消去、否定和辖域收缩扩张等值式，这些等值式在简化和分析一阶逻辑公式时非常关键。 3. 判断公式类型的进一步扩展到一阶逻辑，包括永真式、永假式、矛盾式和可满足式的判断。 4. 使用一阶逻辑自然推理系统F构造推理证明，例如证明涉及到量词的命题，如"每个喜欢步行的人都不喜欢骑自行车"。 这个复习提纲为理解和掌握数理逻辑的基本原理提供了全面的框架，同时也强调了解决实际问题的能力，如通过推理规则解决科研选派问题和日常生活中的逻辑推理。通过深入学习和练习这些内容，可以提升逻辑思维能力和严谨性。