MATLAB在振动信号处理中的应用：预处理与分析

"这篇文档详细介绍了使用MATLAB进行振动信号处理的方法，涵盖了预处理、时域分析、频域分析以及模态参数识别等关键步骤。文档以一号楼楼板的振动信号为例，展示了如何处理加速度数据，以揭示结构对振动的响应。" 在振动信号处理中，MATLAB是一个强大的工具，尤其适用于数据的预处理、分析和建模。文档首先讨论了振动信号预处理的重要性，这一步骤旨在消除噪声和趋势项，以确保数据的准确性。预处理包括两项主要任务： 1. **消除多项式趋势项处理**：由于测量过程中可能出现的零点漂移、环境干扰等因素，原始数据可能包含趋势项。使用最小二乘法可以有效地拟合并去除这些趋势项。在MATLAB中，通过读取数据文件，确定拟合多项式的阶数，然后利用`polyfit`函数计算多项式系数，最后用`polyval`函数减去趋势项，得到趋势项修正后的信号。 2. **采样数据的平滑处理**：平滑处理通常用于滤除高频噪声，常用的方法有移动平均法、滑动窗口滤波等。文档虽然没有详细展开，但在实际操作中，可以使用MATLAB的滤波器设计工具，如`fir1`或`wiener`等函数，来实现信号的平滑。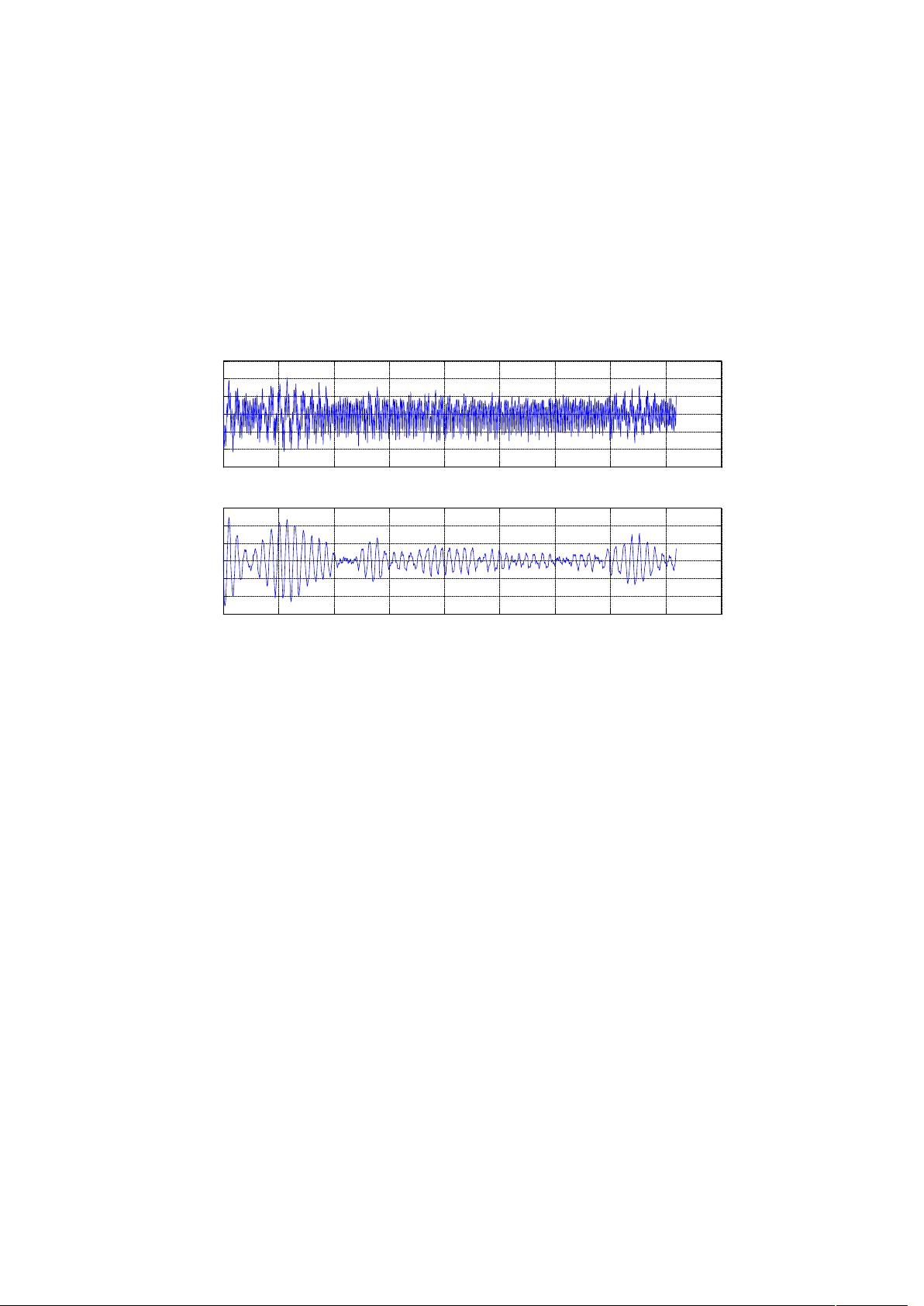 接下来，文档提到了**振动信号的时域和频域处理**： - **时域处理**：通过对时间序列数据进行分析，例如计算均值、标准差、自相关函数等，可以了解信号的基本特征。在MATLAB中，`plot`函数用于绘制时域信号，`grid on`命令添加坐标网格，增强可读性。 - **频域处理**：通过傅里叶变换（如`fft`函数）将信号转换到频域，可以观察信号的频率成分。频谱分析能揭示信号中的周期性和非周期性特征，有助于识别不同振动源。 此外，文档还涉及了**数字信号的生成**和**模态参数的识别**，这在结构动力学中至关重要。模态参数包括固有频率、阻尼比和振型，它们可以通过频域识别（如频谱分析）和时域识别（如自相关分析和希尔伯特黄变换）进行提取。MATLAB提供了诸如`freqresp`（频率响应函数）、`cwt`（小波变换）等工具来辅助这一过程。 这份文档详细阐述了MATLAB在振动信号处理中的应用，从数据预处理到深入分析，为理解和处理类似的振动问题提供了全面的指导。