Matlab入门：探索Monte Carlo方法在实践中的关键要素

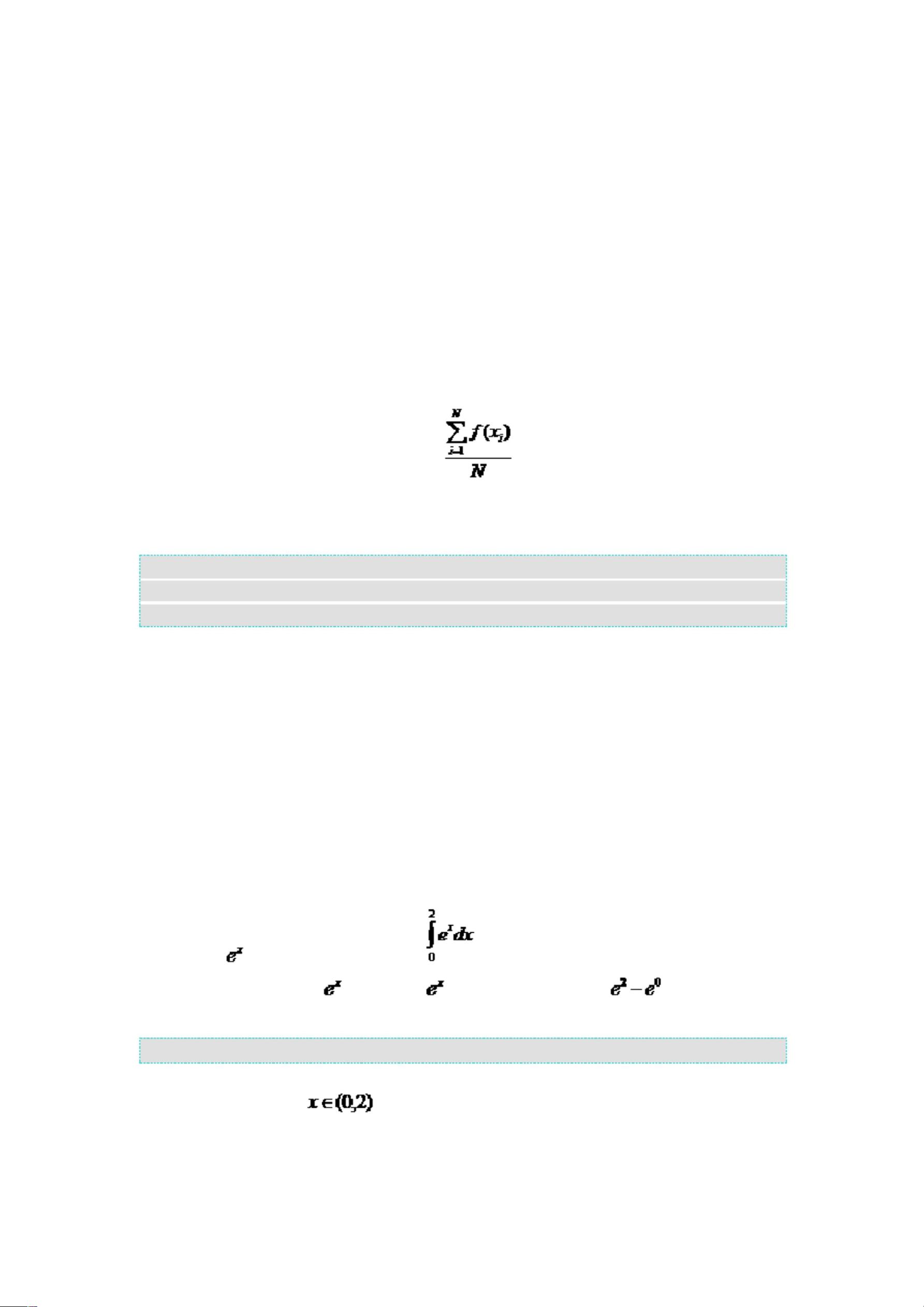
本教程文档名为《基于Matlab语言的Monte Carlo入门教程.docx》，主要介绍了一种广泛应用在各个领域的统计模拟方法——蒙特卡洛方法。该方法看似简单，实则包含丰富的理论和实践细节。首先，作者强调了Monte Carlo方法的核心原理：通过生成大量随机数，通过特定函数运算后取平均，得出近似解决方案。然而，这种方法并非总是适用，其有效性依赖于问题的收敛性、收敛速度、误差分析以及选择合适的算法来提高效率。 在应用过程中，需要关注的关键问题包括： 1. 收敛性：是否能够得到稳定的结果，非收敛问题可能导致计算结果无意义。 2. 收敛速度：尽管通常收敛阶数为1/2，但实际应用中不同算法的效率差异显著。 3. 误差控制：由于是随机性的，必须报告解的方差，以便评估精度。 4. 算法优化：为了减小计算时间，特别是对于实时金融定价等应用，选择高效的算法至关重要。 5. 伪随机数生成：虽然计算机生成的是伪随机数，但理解其潜在影响并生成高质量的随机数至关重要。 6. 理论与实际结合：虽然模型与现实存在差距，但通过科学的方法和调整，可以使Monte Carlo结果更接近实际情况，提升其实用价值。 课程的目标是向非专业背景的学习者提供基础知识，包括但不限于：Monte Carlo方法的基本概念、实例的数学推导、算法实现的步骤、编程细节解读以及误差分析等。考虑到部分学员可能缺乏编程基础，教程特别注重循序渐进的教学方式，逐个解释每个步骤，确保读者能理解整个程序流程。 此外，课程还旨在为学员未来深入学习打下坚实的基础，涵盖了广泛的范围，为他们今后在各自领域运用Monte Carlo方法提供一个扎实的起点。本教程是一份实用性强、兼顾理论深度和编程教学的入门指南，适合希望通过Matlab实现Monte Carlo模拟的初学者。