Copyright (c) 2013 IEEE. Personal use is permitted. For any other purposes, permission must be obtained from the IEEE by emailing pubs-permissions@ieee.org.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication.
5
neighboring solutions. Thereafter, the solutions having larger
crowding distance values are chosen. Here, we r ep lace the
crowding distance operator with the following approach es
(subsections IV-A to IV-E).
A. Classification of Population into Non-dominated Levels
The ab ove procedure of identifying non-dominated f ron ts
using the usual domination principle [17] is also used in
NSGA-III. All popu lation members fro m non-dominated front
level 1 to level l are first included in S
t
.If|S
t
| = N,nofurther
operations are needed and the next generation is started with
P
t+1
= S
t
.For|S
t
| >N,membersfromoneto(l − 1)
fronts are already selected, that is, P
t+1
= ∪
l−1
i=1
F
i
,andthe
remaining (K = N −|P
t+1
|) population members are chosen
from the last front F
l
.Wedescribetheremainingselection
process in the following subsections.
B. Determination of Reference Points o n a Hyper-Plane
As indicated befo re, NSGA-III uses a predefined set of
reference p oints to ensure diversity in obtained solutions.
The chosen reference p oints can either be predefined in a
structured manner or supplied preferentially by the user. We
shall present results of both methods in the results section later.
In the absence o f any preference information, any predefined
structured placement of reference points can be adopted, butin
this paper we use Das and Dennis’s [48] systematic approach
1
that places points on a normalized hyper-plane –a(M − 1)-
dimensional unit simplex – which is equally inclined to all
objective axes and has an intercept of one on each axis. If p
divisions are considered along each objective, the total number
of reference points (H)inanM-objective problem is given
by:
H =
!
M + p − 1
p
"
. (3)
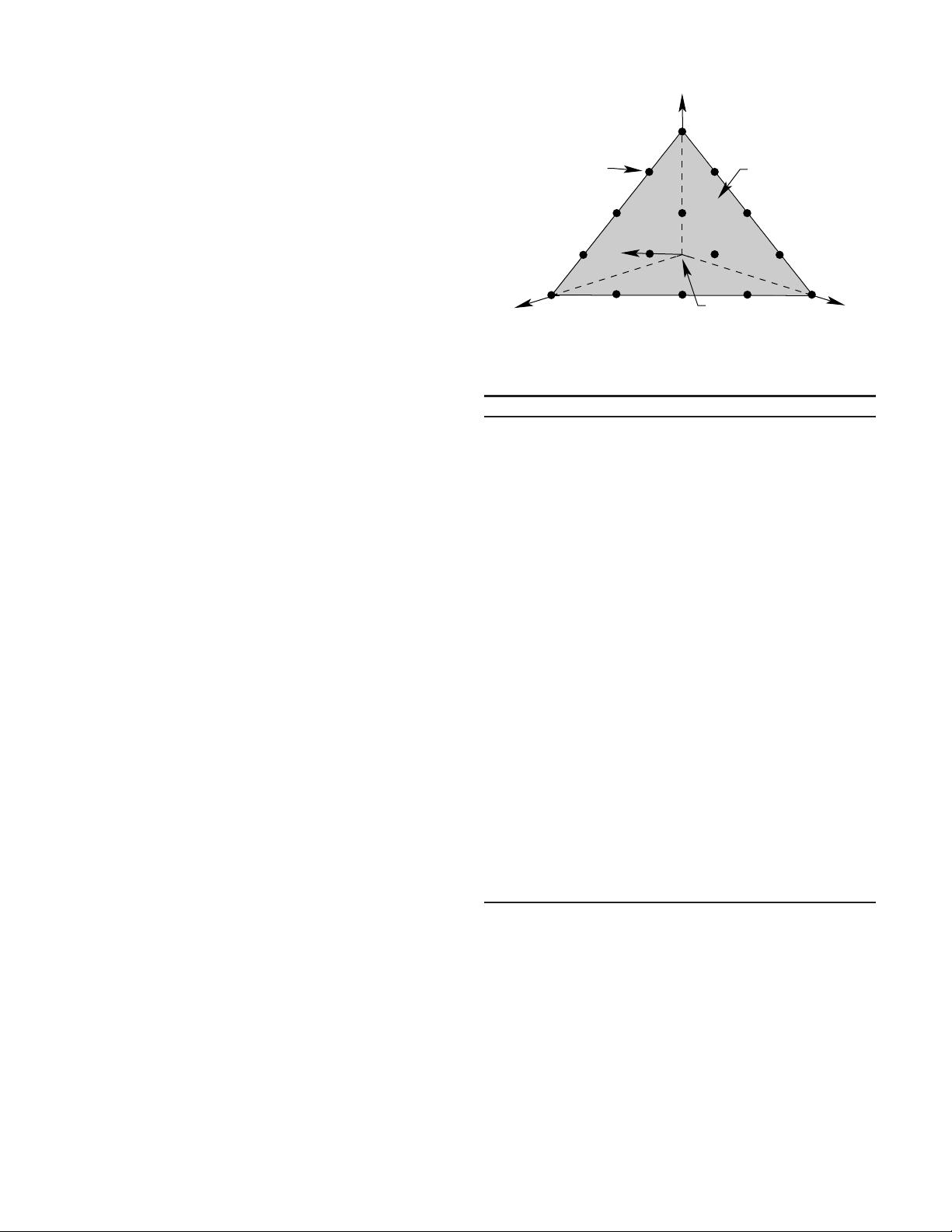
For example, in a three-objective problem (M =3), the
reference points are created on a triangle with apex at (1, 0, 0),
(0, 1, 0) and (0, 0, 1).Iffourdivisions(p =4)arechosenfor
each objective axis, H =
#
3+4−1
4
$
or 15 reference points will
be created. For clarity, these reference points are shown in
Figure 1. In the proposed NSGA-III, in addition to emphasiz-
ing non-dominated solutions, we also emphasize population
members which are in some sense associated with each
of these reference points. Since the above-created reference
points are widely distributed on the entire normalized hyper-
plane, the obtained solutions are also likely to be widely
distributed on or near the Pareto-optimal front. In the case of a
user-supplied set of preferred reference points, ideally the user
can mark H points on the normalized hyper-plane or indicate
any H, M -d imensional vectors for the purpose. The proposed
algorithm is likely to find near Pareto-optimal solutions cor-
responding to the supplied reference points, thereby allowing
this method to be used more from the point of view of a
combined application of decision-making and many-objective
optimization. The procedure is presented in Algorithm 1.
1
Any other structured distribution with or without a biasing on some part
of the Pareto-optimal front can be used as well.
hyperplane
Normalized
line
Reference
point
Reference
Ideal point
1
1
f1
f3
1
f2
Fig. 1. 15 reference points are shown on a normalized reference plane for
athree-objectiveproblemwithp =4.
Algorithm 1 Generation t of NSGA-III procedure
Input: H structured reference points Z
s
or supplied aspira-
tion points Z
a
,parentpopulationP
t
Output: P
t+1
1: S
t
= ∅, i =1
2: Q
t
= Recombination+Mutation(P
t
)
3: R
t
= P
t
∪ Q
t
4: (F
1
,F
2
,...)=Non- dominated-sor t(R
t
)
5: repeat
6: S
t
= S
t
∪ F
i
and i = i +1
7: until |S
t
|≥N
8: Last front to be included: F
l
= F
i
9: if |S
t
| = N then
10: P
t+1
= S
t
,break
11: else
12: P
t+1
= ∪
l−1
j=1
F
j
13: Points to be chosen from F
l
: K = N −|P
t+1
|
14: Normalize objectives and create reference set Z
r
:
Normalize(f
n
,S
t
,Z
r
,Z
s
,Z
a
)
15: Associate each membe r s of S
t
with a reference point:
[π(s),d(s)] =Associate(S
t
,Z
r
) % π(s):closest
reference point, d:distancebetweens and π(s)
16: Compute niche count of reference point j ∈ Z
r
: ρ
j
=
%
s∈S
t
/F
l
((π(s)=j)?1 : 0)
17: Choose K members o ne at a time from F
l
to construct
P
t+1
: Niching(K, ρ
j
,π,d,Z
r
,F
l
,P
t+1
)
18: end if
C. Adaptive Normalization of Population Members
First, the ideal point of the population S
t
is determined
by identifying the minimum value (z
min
i
), for each objective
function i =1, 2,...,M in ∪
t
τ =0
S
τ
and by constructing the
ideal point ¯z =(z
min
1
,z
min
2
,...,z
min
M
).Eachobjectivevalue
of S
t
is then translated by subtracting objective f
i
by z
min
i
,
so that the ideal point of translated S
t
becomes a zero vector.
We denote this translated objective as f
$
i
(x)=f
i
(x) − z
min
i
.
Thereafter, the extreme po int in each objective axis is identi-
fied by finding the solution (x ∈ S
t
)thatmakesthefollowing
achievement scalarizing function minimum with weight vector









