IEEE COMMUNICATIONS LETTERS, VOL. 17, NO. 2, FEBRUARY 2013 337
Energy Efficiency Optimization for
Cognitive Radio MIMO Broadcast Channels
Junling Mao, Gang Xie, Member, IEEE, Jinchun Gao, Member, IEEE, and Yuanan Liu, Member, IEEE
Abstract—Conventional designs of cognitive radio (CR)
multiple-input multiple-output (MIMO) systems mainly focus
on the system throughput. Since nowdays the energy efficiency
(EE) of wireless systems has become more and more important,
this paper intends to improve the system throughput for unit-
energy consumption in CR MIMO broadcast channels (BC). The
EE optimization problem of CR MIMO BC is studied under
the total power constraint, the interference power constraint
and the minimum system throughput constraint. Since the EE
optimization problem is non-convex, in order to find the optimal
solution, we transform it into an equivalent one-dimension
problem with a quasi-concave objective function and use the
golden section method to solve it. Through simulations, we show
the efficiency of the proposed algorithm.
Index Terms—Energy efficiency, cognitive radio, MIMO broad-
cast channels, power allocation.
I. Introduction
C
OGNITIVE Radio (CR) technique is first introduced by
Mitola [1] and has drawn considerable attentions due
to its advantage of spectrum reusing. In CR networks, the
secondary networks usually communicate over the spectrum
originally allocated to primary networks while ensuring that
the performance degradation of the active primary transmis-
sions is tolerable [2].
Recently, the multiple antennas technique is introduced to
CR networks to improve the system throughput of secondary
systems [3]. [4] and [5] give the optimal power allocation for
CR MIMO broadcast channels (BC) based on the dirty paper
coding (DPC) scheme [6] which can achieve the capacity of
MIMO BC [7]. Since the power allocation problem of CR
MIMO BC is non-convex, [4] and [5] solve it via the multiple
access channels (MAC) - BC duality of CR MIMO BC.
Besides the system throughput (or the spectrum efficiency
(SE)), the energy efficiency (EE) (or the system throughput
for unit-power consumption) has been considered more and
more important in future wireless systems [8][9][10]. The EE
optimization problem of non-CR MIMO BC has been solved
in [11] based on the fractional programming theory, the convex
optimization theory [12] and the MAC-BC duality of non-CR
MIMO BC. However, the EE optimization problem of CR
Manuscript received October 22, 2012. The associate editor coordinating
the review of this letter and approving it for publication was W. Zhang.
This work was supported in part by Canada-China Scientific and Techno-
logical Cooperation (No. 2010DFA11320), the Natural Science Foundation of
China (Nos. 60973111 and 61170275), and Important National Science and
Technology Specific Projects (No. 2012ZX03003001-004).
J. Mao, J. Gao. and L. Liu are with the Beijing Key Laboratory of Work
Safety Intelligent MonitoringBeijing University of Posts and Telecommuni-
cations, Beijing 100876, China (e-mail: maojunling@bupt.edu.cn).
G. Xie is with the Beijing Key Laboratory of Network System Architecture
and Convergence, Beijing University of Posts and Telecommunications.
Digital Object Identifier 10.1109/LCOMM.2012.121912.122351
DPC
Secondary Transmitter
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
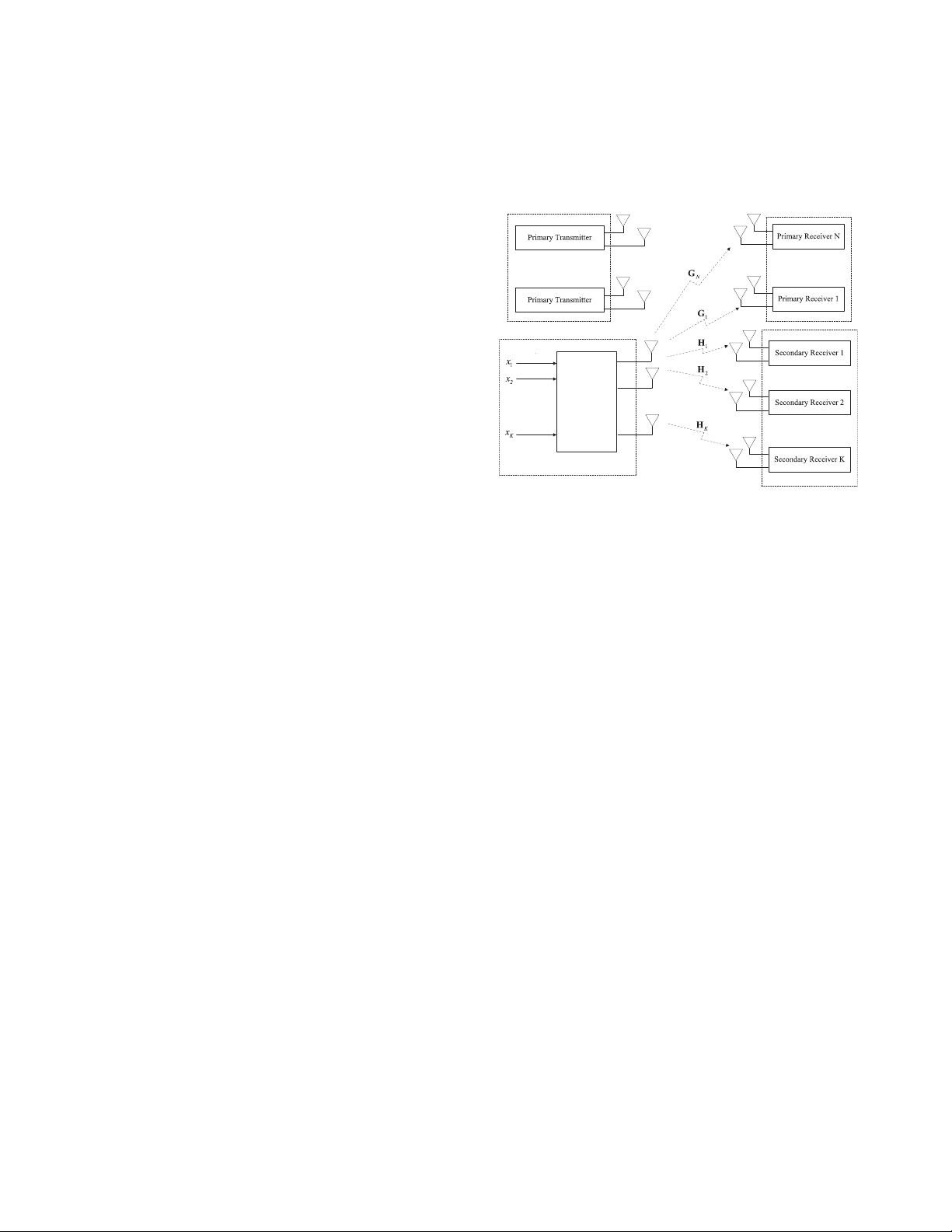
Fig. 1. The system model of CR MIMO BC.
MIMO BC is still unsolved in previous works.
In this paper, we study the EE optimization of CR MIMO
BC based on the MAC-BC duality of CR MIMO BC.
To protect the primary transmission, both the total power
constraint and the individual interference power constraint
applied at each primary receiver are considered. Since the
EE optimization of MIMO BC is more complicated than that
of non-CR MIMO BC, the optimization method used in this
paper is totally different from the method used in [11]. In this
paper, an equivalent one-dimension optimization problem with
quasi-concave objective function is constructed to solve the EE
optimization problem of CR MIMO BC. Note that although
the method used in this paper is similar to the method in [13]
which also constructs an equivalent problem to optimize EE,
the proposed method has wider applicability since it does not
restrict the concavity and differentiability of the rate function.
The rest of paper is organized as follows. Section II provides
the system model of CR MIMO BC. Section III presents
the optimal power allocation scheme. The simulation results
and conclusions are given in Section IV and Section V
respectively.
The following notations are used in this paper. |·| denotes the
determinant,
(
·
)
†
denotes the conjugate transpose and A 0
means that A is semi-definite positive. The identity matrix
is denoted by I. The distribution of a circularly-symmetric-
complex-Gaussian (CSCG) matrix with the mean Z and the
covariance Σ is denoted by CN
(
Z, Σ
)
.
II. System Model
This paper considers the CR MIMO BC as shown in Fig.
1, where one secondary transmitter (ST) and K secondary
receivers (SRs) share the spectrum with N primary users (PUs)
1089-7798/13$31.00
c
2013 IEEE


















