初学者二次函数解析与习题集

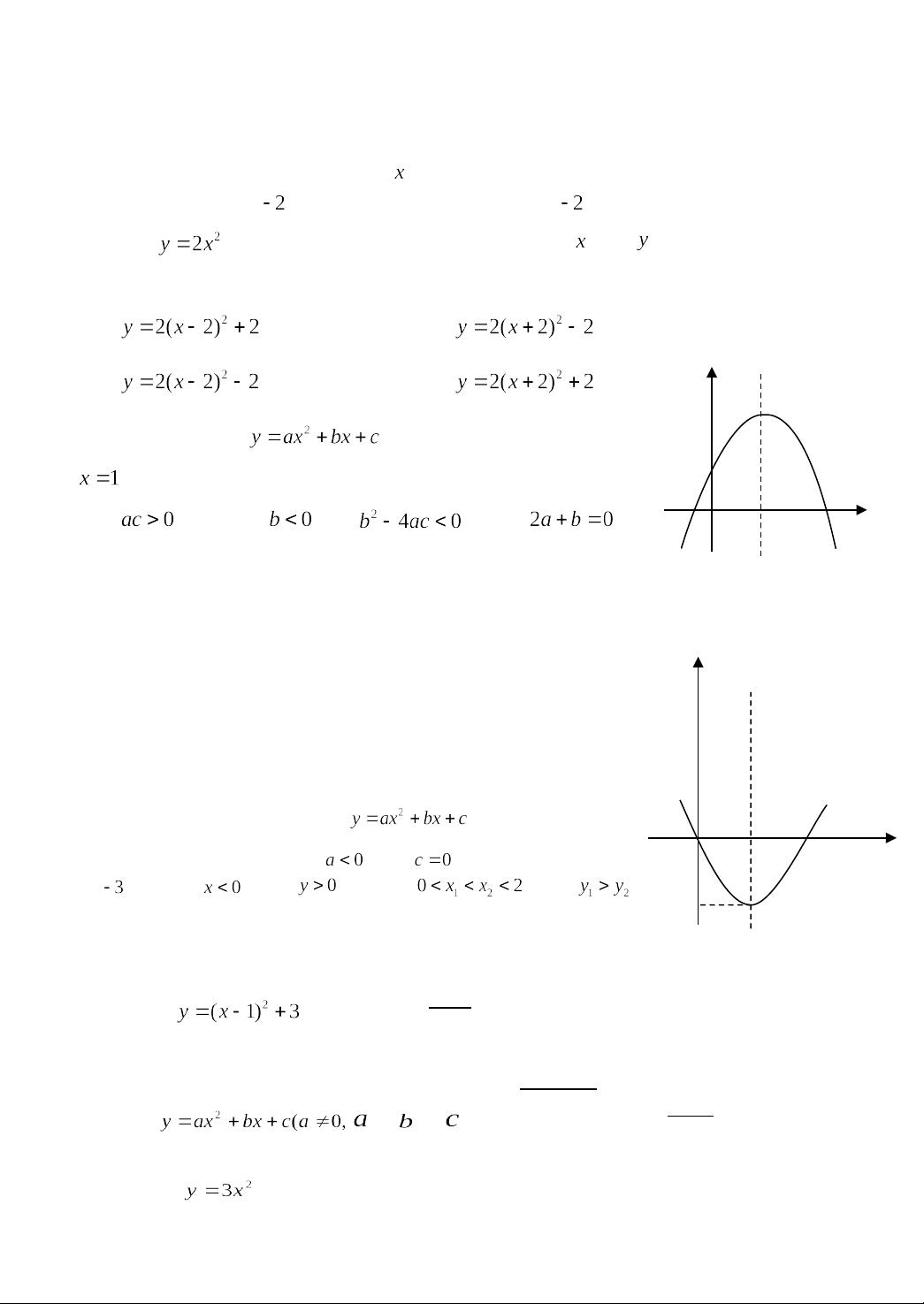
"这篇文档是一份关于二次函数的练习题集，旨在帮助中学生巩固和深化对二次函数的理解。这份资料包含选择题、填空题和解答题，涵盖了二次函数的基本概念，如图象特征、顶点坐标、对称轴、函数解析式以及图形平移等知识。" 二次函数是初中数学中的核心概念，它是一种形式为y = ax^2 + bx + c (a ≠ 0) 的函数，其中a决定了开口方向（a>0开口向上，a<0开口向下），b决定对称轴的位置（x=-b/2a），c决定函数在y轴的截距。这份练习题旨在帮助初学者掌握以下关键知识点： 1. **图象与轴的交点**：例如题1询问二次函数y=x^2+x-2与x轴的交点，解这类题目通常需要通过解方程x^2+x-2=0找到x轴交点的横坐标。 2. **坐标轴平移**：如题2，抛物线不动，坐标轴平移后，函数解析式会有所变化，需要根据坐标轴平移规则进行转换。 3. **对称轴与顶点**：题3中，通过图象判断二次函数的对称轴及顶点，对称轴由x=-b/2a给出，顶点坐标为(-b/2a, c - b^2/4a)。 4. **顶点坐标与对称轴**：题4考察了如何从一般形式找到顶点坐标和对称轴，顶点坐标为(0, -d)，对称轴为x=0，其中d=c/a。 5. **顶点在x轴上**：题5中，抛物线的顶点在x轴上意味着顶点的y坐标为0，可以利用顶点公式求解k的值。 6. **函数最值**：题6通过配方法或公式法确定二次函数的最小值，对于y=ax^2+bx+c (a>0)，最小值为c-b^2/(4a)。 7. **函数信息判断**：题7要求学生从图象中提取信息，如对称轴、最小值等，并检验这些信息的正确性。 8. **顶点坐标**：填空题8要求找出抛物线的顶点坐标，这需要通过配方或计算对称轴来确定。 9. **二次函数解析式**：题9通过已知的三个点（顶点和两个x轴交点）确定函数解析式，可以使用待定系数法。 10. **对称轴与顶点坐标**：题10询问函数的对称轴和顶点坐标，这需要对一般形式进行转换。 11. **函数图象平移**：题11涉及到函数图象的平移，平移后的顶点坐标和对称轴可以通过原坐标加上相应的平移量得出。 12. **代入法求解析式**：题12利用点(－1，-3)代入二次函数y=ax^2求解a的值，从而得到解析式。 13. **函数性质**：题13要求选取参数使得函数满足特定性质，如开口方向和增减性，需要结合函数图像和性质进行选择。 14. **交点坐标**：题14询问二次函数与x轴和y轴的交点坐标，通过解方程组得到。 15. **解答题**：这部分可能包含更复杂的问题，如求解函数解析式、分析函数性质等，需要综合运用二次函数的知识来解答。 通过完成这些练习题，学生不仅可以熟悉二次函数的基本性质，还能提升解决实际问题的能力，为后续的学习打下坚实基础。