PCA算法解析:MATLAB实现数据降维
版权申诉
86 浏览量
更新于2024-08-03
收藏 112KB DOCX 举报
"matlab PCA 数据降维 主成分分析 PCA算法 实现 源码 验证"
主成分分析(PCA)是一种常用的数据分析方法,主要用于高维数据的降维。PCA通过线性变换将原始数据转换为一组各维度线性无关的表示,新坐标轴按数据方差大小排序,使得数据在低维空间中的投影仍能保留原始数据的大部分信息。PCA在机器学习、图像处理、生物信息学等领域有着广泛应用。
在MATLAB中,PCA可以通过内置函数`pca`实现。该函数接受一个数据矩阵作为输入,返回多个输出参数,包括:
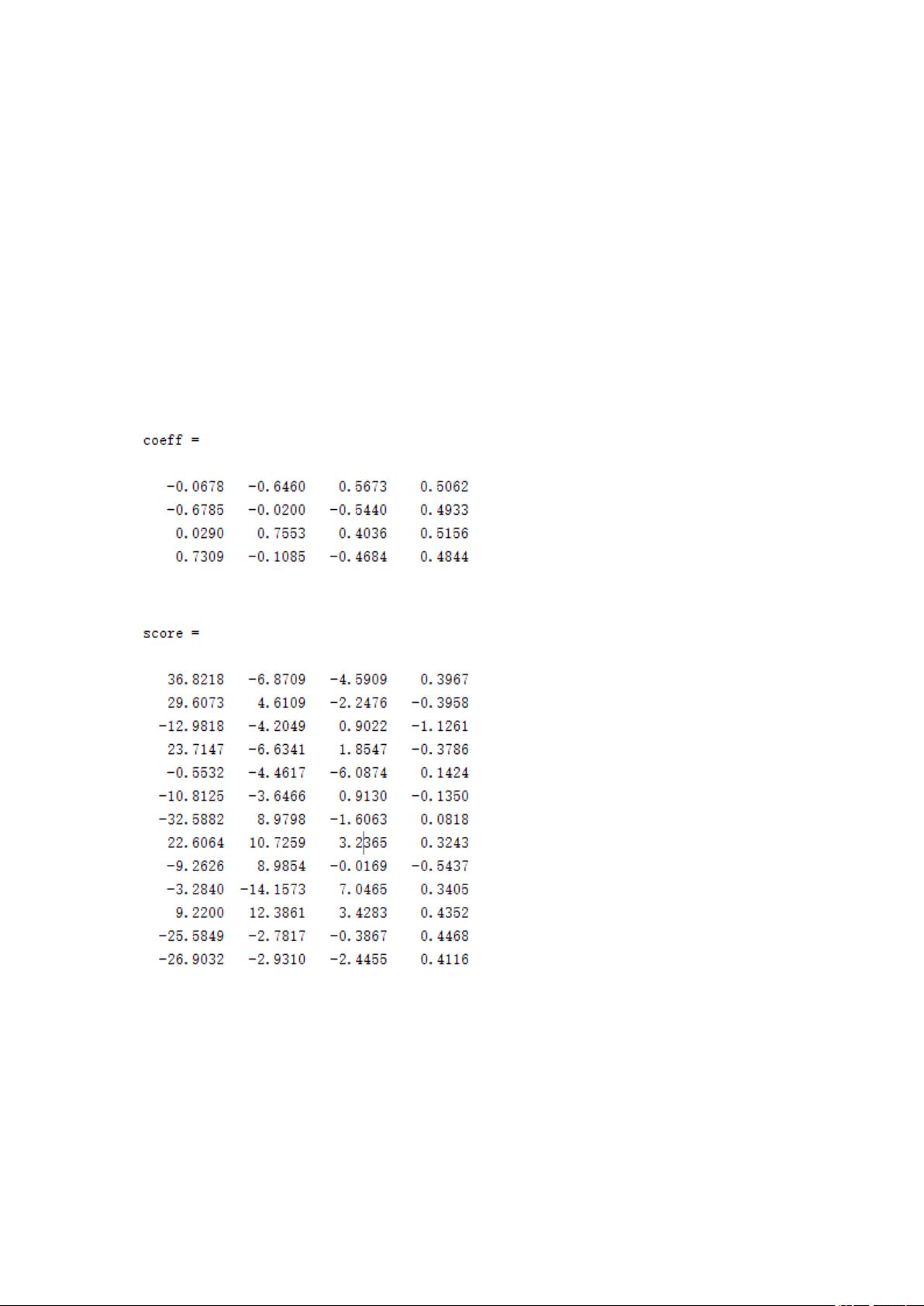
1. `coeff`: 主成分系数矩阵,即特征向量,按照特征值大小排序。这些向量定义了新的坐标轴。
2. `score`: 主成分分数矩阵,表示原始数据在主成分坐标系下的投影,即标准化数据乘以`coeff`。
3. `latent`: 特征值向量,对应于每个主成分的方差。
4. `tsquared`: Hotelling’s T-squared统计量,用于异常检测,表示标准化得分的平方和。
5. `explained`: 各主成分解释的总方差比例,反映了每个主成分对数据变异的贡献程度。
6. `mu`: 输入数据的均值向量,用于数据标准化。
在PCA的执行过程中,首先需要对数据进行预处理,通常是进行零均值化(减去均值),以消除数据尺度的影响。然后计算数据的协方差矩阵,接着找到协方差矩阵的特征值和对应的特征向量。特征值代表了各个主成分的方差,特征向量则指示了主成分的方向。通常选择方差最大的几个特征值对应的特征向量作为主成分。
在MATLAB的`pca`函数中,特征值和特征向量可能已经按降序排列,但有时需要手动调整。如果特征向量与预期的主成分系数不一致(例如,第二个主成分取负号),可以通过调整特征向量的顺序或改变特征向量的符号来匹配。
为了验证PCA的正确性,可以手动实现PCA的过程,包括数据标准化、计算协方差矩阵、求解特征值和特征向量,然后比较手动计算的结果与`pca`函数的输出是否一致。在示例中,通过对比`score`和手动计算的`score_1`,可以确认PCA的正确性。
PCA是一种强大的数据分析工具,MATLAB的`pca`函数提供了一种便捷的方式来执行PCA并获取相关统计信息。理解PCA的原理和MATLAB的实现细节,对于有效应用PCA进行数据降维和特征提取至关重要。
2024-04-28 上传
354 浏览量
106 浏览量
2024-04-28 上传
2024-04-28 上传
172 浏览量
292 浏览量
171 浏览量
161 浏览量
211 浏览量

手把手教你学AI
- 粉丝: 9587
最新资源
- Profwiz3:快速迁移域控用户配置的神器
- Flutter新项目入门指南与资源分享
- C#串口通信实践:开启/关闭、数据传输及波特率设置
- Phoenix BIOS Editor 2.2.6.0:Windows平台的BIOS编辑工具安装指南
- 多周期CPU制作与烧制到basy3板子的实操指南
- 易语言实现11选n组合源码解析
- NC冠状病毒数据分析仪表板的构建与应用
- NetworkEye:全方位监控App内HTTP请求工具
- PowerShell脚本分享:marino-scripts的使用体验
- 探索ArcGIS 10.3:下载与应用指南
- 深入解析恒压供水系统及其变频器转换线路
- Android平台下的拉刷新技术详解
- 掌握ASP.NET:动态网站开发教程第三版
- 使用fileMagic_RoboCopyPS PowerShell脚本按文件标头快速搜索和复制文件
- iOS APP引导页设置教程与SYGuideView组件使用
- 全面测试的旅游机票订购网站系统开发