机器人静力与动力学分析：力矩平衡与雅可比矩阵

"该资源为‘静力学和动力学分析.pptx’，主要探讨了机器人在静力学和动力学方面的分析，涉及机器人操作臂力的平衡以及力雅可比矩阵的理论。" 在机器人技术中，静力学和动力学分析是至关重要的概念，它们帮助我们理解和设计机器人的运动和交互能力。首先，机器人静力分析关注的是机器人在工作时与环境之间的相互作用力和力矩。这些力和力矩由各个关节的驱动装置产生，通过连杆传递到末端执行器，以克服外部环境的作用力。理解这种关系是实现机器人操作臂力控制的基础。 在静力平衡的讨论中，我们考虑了如下的力和力矩关系。例如，杆i通过关节i与i-1和i+1相连，存在作用力fi-1，i和力矩ni-1，i，以及反作用力和力矩。同样，对最末杆的力和力矩fn，n+1表示机器人与环境的交互，而-fn，n+1和-nn，n+1则代表环境对机器人的反作用。此外，还有机器人基座对第一杆的作用力和力矩f0，1及n0，1，以及连杆自身的重力mig。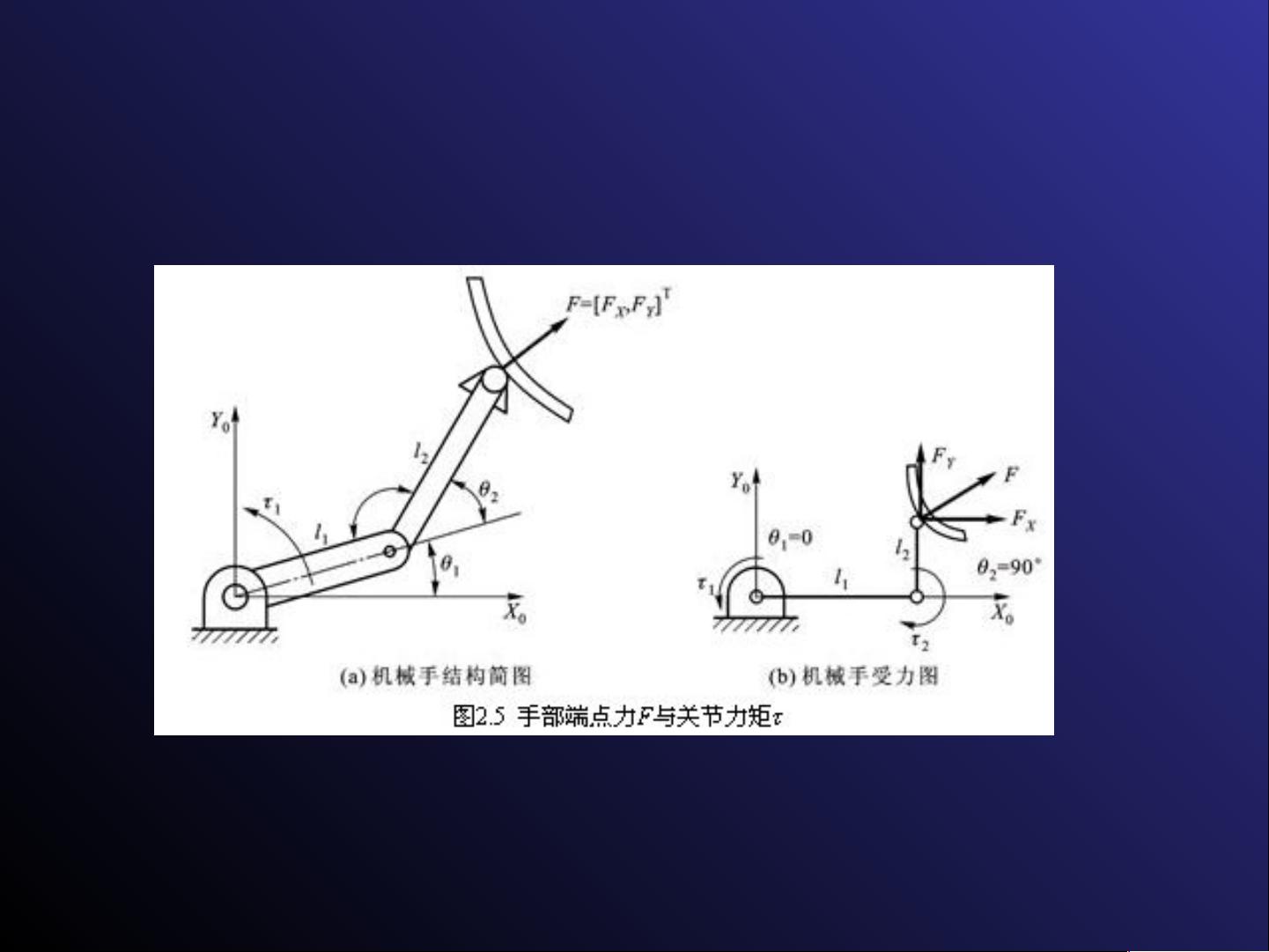 在动力学分析中，机器人力雅可比矩阵（Force Jacobian Matrix）是一个关键工具，它用于简化表示末端执行器的力和力矩，通常称为端点广义力F。这个6维矢量包括了对外界环境的作用力和力矩。同时，关节驱动力或力矩可以表示为n维矢量τ，其中τi代表每个关节的驱动力矩或力。对于旋转关节，τi是力矩；对于平移关节，τi是力。 虚功原理在此过程中扮演了核心角色，它帮助我们推导出手部端点力F与关节力矩τ之间的关系。通过计算在虚拟位移下力和力矩所做的功，我们可以找到机器人处于静态平衡的必要条件，即所有虚功之和为零。这导致了一个线性映射关系，即静态平衡状态下，手部端点力F与广义关节力矩τ之间的关系，通常表示为F = J^T * τ，其中J是雅可比矩阵。 通过这样的分析，工程师能够设计和控制机器人，确保它们在各种任务中能够正确地施加和承受力，同时满足动力学和静力学的平衡条件。这对于实现精确的运动控制、避免过载以及优化能量效率至关重要。在实际应用中，这些理论不仅应用于机器人设计，还广泛用于机器人路径规划、力控制策略和碰撞检测等领域。