动态边长图与p-adic AdS/CFT中的曲率动力学与全息计算

85 浏览量更新于2024-07-16 收藏 623KB PDF 举报

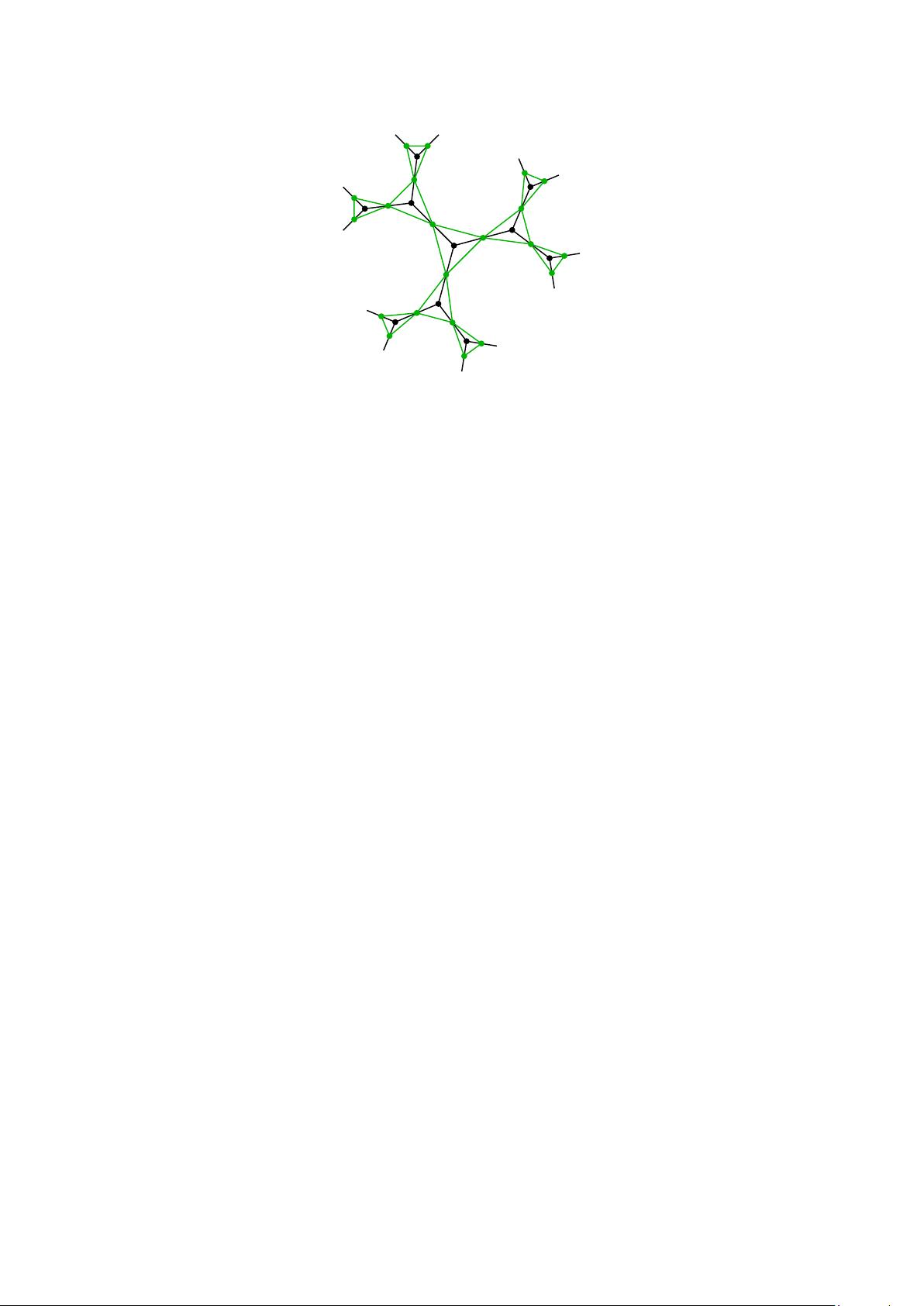
本文主要探讨了图的边缘长度动力学及其在p-adic AdS/CFT（p-adic Anti-de Sitter/Conformal Field Theory）框架下的应用。作者们构建了一套基于可变边长图上的Ricci曲率概念的理论，这是一种欧几里得理论，其目的是为爱因斯坦-希尔伯特引力作用的离散形式提供一个数学描述。在这个理论中，他们着重考虑的是树形图，因为这样的结构能够保证在建立离散引力模型时满足必要的条件。作者们强调，所有的图必须要么是一棵树，要么其周期长度足够长，这有助于保持理论的稳定性。特别地，他们提到了所有边长相等的无限规则树，这些树具有恒定的负曲率，它们在p-adic AdS/CFT中扮演了类似于经典AdS空间中de-Sitter空间的角色。在p-adic背景下，这样的结构对于理解和模拟量子引力现象具有重要意义。核心研究内容包括了从全息图的角度分析边缘长度的波动如何影响算子的行为。这个算子的维数与边界维度相匹配，表现出与应力张量类似的特性，这表明它在理论中扮演着关键的角色。通过这样的计算，作者们揭示了边缘长度动力学如何映射到量子场论中的物理效应，这对于探索p-adic AdS/CFT中的新型物理现象具有潜在的价值。这篇论文不仅发展了图的边缘长度动力学理论，还将其成功地应用于p-adic AdS/CFT的框架，从而推进了我们在量子引力和非欧几何领域的理解。文章发表于《Journal of High Energy Physics》（JHEP），并得到了同行们的广泛认可，接收和接受时间分别为2017年5月和6月，最终在6月底正式发布。参与研究的学者们来自多个知名机构，如普林斯顿大学、加州理工学院和德国海德堡大学等，他们的贡献表明了这一领域跨学科研究的活跃与深度。

JHEP06(2017)157

Figure 1. A regular graph in black, and its line graph in green.

To make the edge Laplacian (2.5) seem more natural, consider the line graph L(G)

of an undirected graph G. By deﬁnition, every vertex of L(G) corresponds to an edge of

G, and two vertices of L(G) are connected by an edge precisely if the corresponding two

edges of G meet at a vertex. Essentially by inspection, the edge Laplacian (2.5) on G is the

standard vertex Laplacian d

†

d on L(G). It is interesting to note that the line graph of T

comprises many copies of the complete graph on q + 1 elements, tied together by sharing

each vertex between two copies: see ﬁgure 1.

3 Ricci curvature on graphs

While the action (1.3) seems natural enough from the point of view of dynamical models

on graphs, we would prefer to have some geometrical starting point that would allow us

to identify a graph-theoretic analog of the Einstein-Hilbert action. At ﬁrst it seems like

a hopeless task to construct such an action on a tree graph, because the Einstein-Hilbert

action involves the Ricci scalar R, which is usually constructed as a contraction of the

Riemann tensor R

µν

. But R

µν

is generally thought of as the ﬁeld strength of the

Christoﬀel connection; in other words, it describes holonomies around small loops. With

no loops, it’s hard to see how to deﬁne non-trivial ﬁeld strengths. To avoid this, we want

to take advantage of constructions of analogs of the Ricci tensor R

µν

that do not depend

on connections at all, but instead on some notion of transport distance.

To build intuition, let’s recount a standard result (see for example [10]) that goes in

the direction we want, but which is framed in the context of a smooth D-dimensional

manifold with a Euclidean metric which induces a distance function d(x, y) between any

two points on the manifold. Given two points x

and y

, separated by a small distance

r, choose some much smaller distance a  r and consider balls B

and B

, comprising

all points x with d(x, x

) < a and all points y with d(y, y

) < a, respectively. Let n

the unit vector in the direction from x

to y

; we are not concerned with exactly which

tangent space n

lies in because we wish to use it in an asymptotic formula which can

absorb O(r) uncertainties in n

. Likewise we consider the Ricci curvature R

µν

at x

or y

– 6 –

剩余34页未读，继续阅读

weixin_38556541

粉丝: 6
资源: 970

动态边长图与p-adic AdS/CFT中的曲率动力学与全息计算

图像边缘宽度

张量网络和（p-adic）AdS / CFT

p-adic AdS / CFT中的Wilson线网络

p-adic CFT是全息张量网络

P-adic_Calculator:提供指定有理数和素数的 p-adic 展开

论文研究 - 从变形理论的角度研究p-Adic Frobenius升力和p-Adic周期

p-adic numbers, p-adic analysis, and zeta-functions 2nd ed. - N. Koblitz

p_adic_order(N,p):此函数计算有理数 N 的 p-adic 估值（相当于 p-adic 阶数）-matlab开发

p-adic.github.io:这是我的圈子“p-adic爱圈”的主页

p-adic度量空间中整数距离测量的流处理方法

最新资源