欧拉角与坐标转换：从欧氏到地心坐标系的详细解析

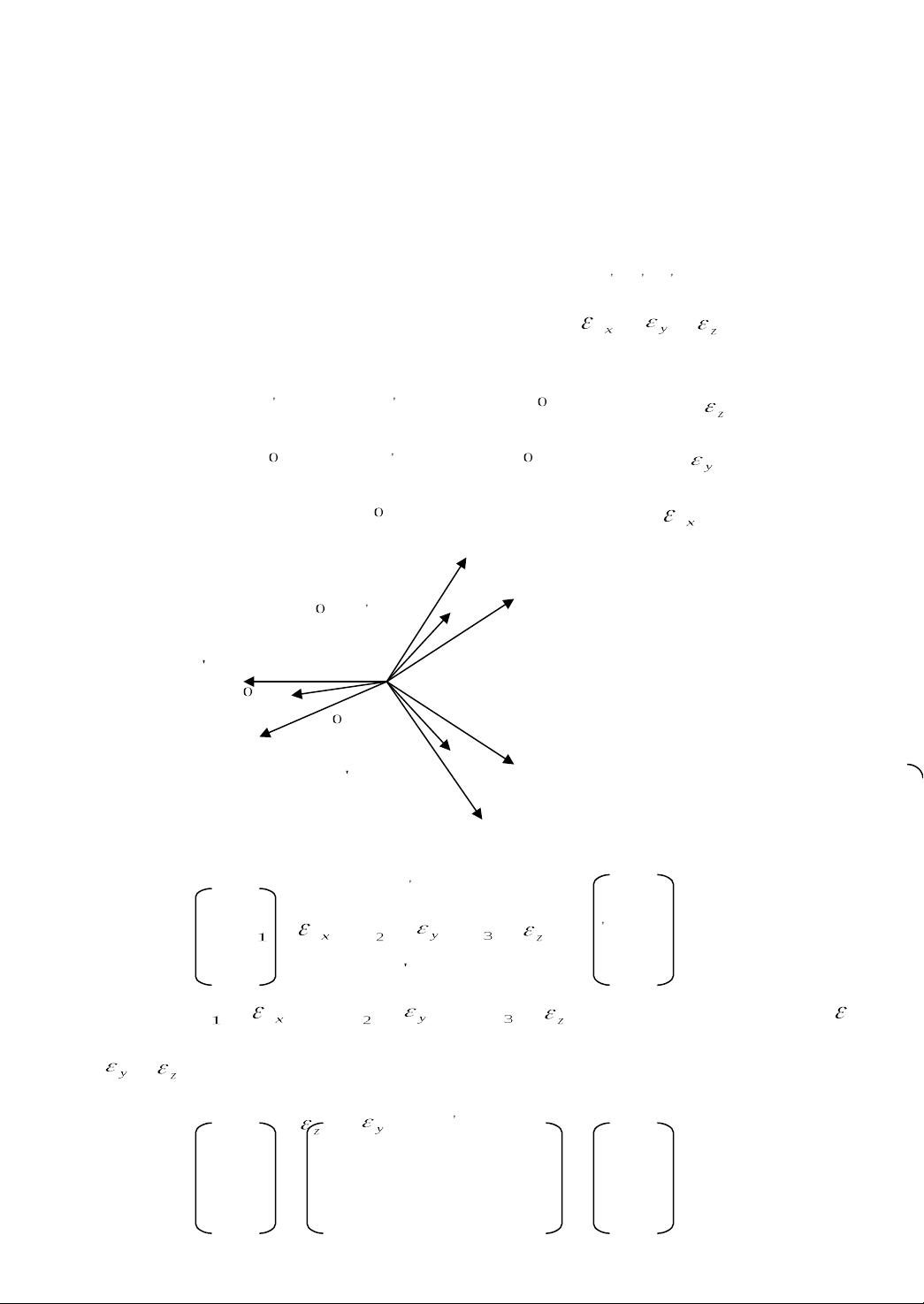
本资源主要探讨了坐标转换模型，特别是在空间坐标系统之间的转换。首先，针对平面坐标基准转换，以欧拉角（即旋转参数）作为关键概念，解释了如何通过三次旋转将两个不同的空间直角坐标系O-XYZ和O-X[pic]Y[pic]Z[pic]重合。具体步骤包括绕OZ轴旋转至OZ[pic]轴，分别旋转角度为[pic]、[pic]和[pic][pic]，通过旋转矩阵R[pic]([pic][pic])、R[pic]([pic])和R[pic]([pic])来实现，当旋转角度足够小的时候，这些矩阵可以用简化公式来表示。 接着，资源深入讨论了GPS测量常用的WGS-84地心坐标系与国家大地坐标系（如1980年坐标系）以及北京坐标系（如1954年坐标系）之间的转换。在这种情况下，除了平移参数[pic]X[pic]、[pic]Y[pic]、[pic]Z[pic]，用于表示两个坐标系原点之间的相对位置，还涉及到三个旋转参数[pic][pic]、[pic]和[pic]，它们在坐标轴不平行的情况下用来描述坐标系的非平行变换。 总结来说，这部分内容着重于理解不同坐标系统之间的转换原理，包括欧拉角的运用、旋转矩阵的表达以及平移和旋转参数的定义，这对于处理涉及多个坐标系转换的地理信息系统（GIS）和导航技术尤为重要。掌握这些模型有助于在实际工作中正确处理数据，确保测量结果的一致性和准确性。