MATLAB解常微分方程： ode45与龙格库塔法

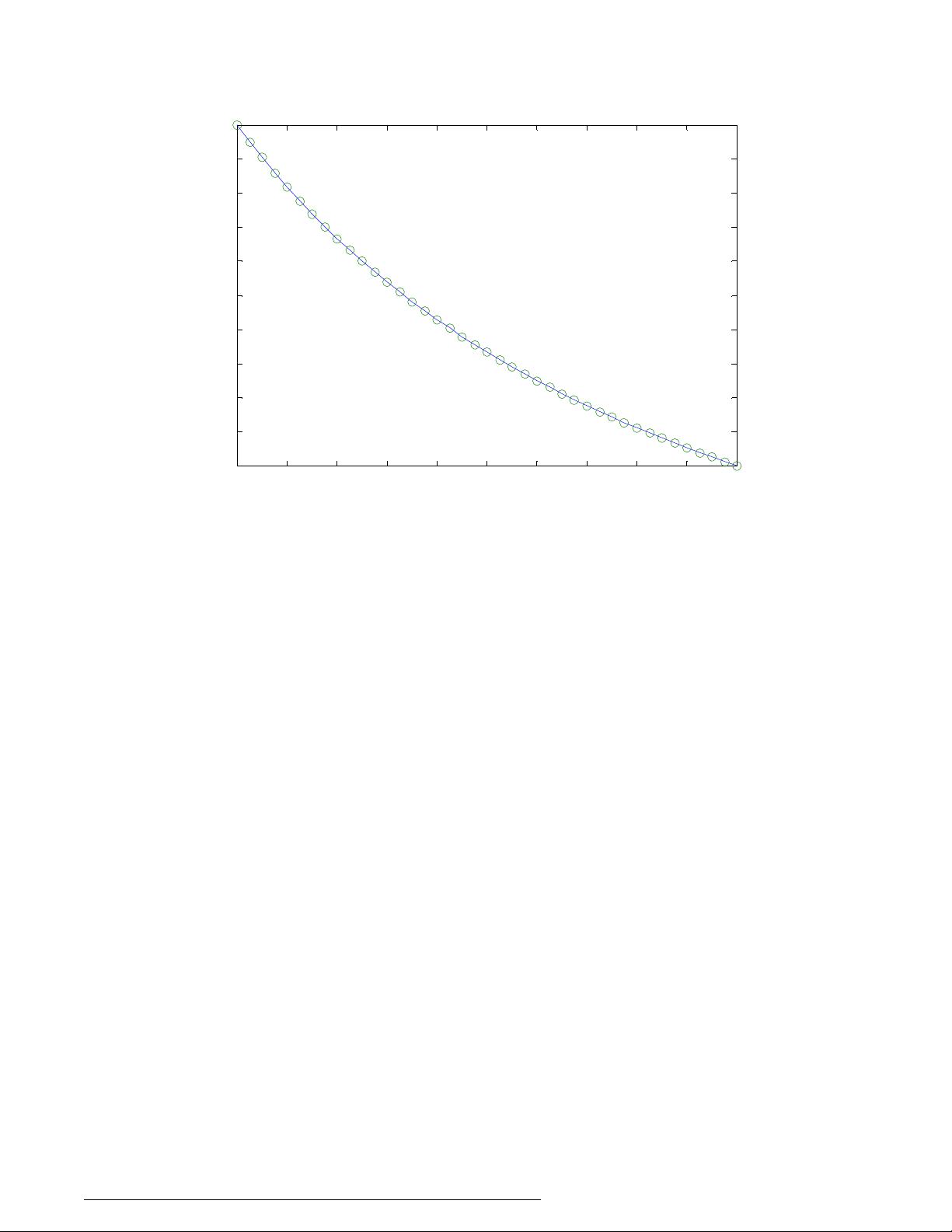
"本文主要介绍了如何在MATLAB中使用龙格库塔法解微分方程，特别是关于ode23和ode45等函数的使用方法以及相关设置选项的介绍。" MATLAB提供了多种工具来解决常微分方程（ODE），其中最常用的是基于龙格库塔法的求解器。龙格库塔法是一种数值积分方法，用于近似求解初值问题的微分方程。MATLAB中的ode23和ode45函数分别采用了二阶和四阶的龙格库塔方法，其中ode45由于其良好的稳定性和精度，通常被视为首选方法。 ode23函数适用于解决二、三阶的微分方程组，而ode45则使用了四、五阶的龙格库塔-芬尔格方法，提供更高的精度。这些函数的工作原理是根据解的变化情况自动调整步长，以确保在解的平滑区域减少计算点，而在解快速变化的地方增加计算点，从而达到平衡效率和精度的目的。 在使用这些函数时，你需要定义一个M文件，该文件包含微分方程的定义。例如，函数`myode(t,x)`应返回向量`x'`，即`x`关于`t`的导数。然后，你可以调用相应的求解器，如`[t,x]=ode45('myode',[t0,tf],x0)`，其中`t0`和`tf`分别是初始时间和终止时间，`x0`是初始条件。 MATLAB还提供了其他一些求解器，如ode113，适用于高阶或大规模的微分方程；ode23t、ode23s和ode15s针对不同复杂度的问题提供了不同级别的精度和稳定性；ode23tb则是对ode23s的一个改进，特别适合常量矩阵存在的系统。 在求解微分方程时，可以通过odeset函数设置求解器的参数，如步长控制、容差等。odeset允许用户自定义各种选项，以适应特定的求解需求。例如，`options=odeset('RelTol',1e-6,'AbsTol',1e-9)`会设置相对容差和绝对容差。通过odeget函数，可以检索已设置的参数。 MATLAB的微分方程求解工具提供了强大的灵活性和适应性，能够处理各种类型的微分方程问题，并通过用户可配置的参数来优化解的质量和计算效率。了解和熟练掌握这些工具对于在MATLAB环境中进行数值模拟和科学计算至关重要。