A Method Of Indoor Multi-path IR-UWB
Localization Based On Bayesian Compressed Sensing
Wang Ping, Ruan Huailin, Fan Fuhua
Electronic Engineering Institute, Hefei, China, 230037
Email:wangping918304@163.com
Abstract—In order to solve the problem that high sampling rates
of ADC which limit ultra-wideband (UWB) localization accuracy,
a method of UWB localization based on Bayesian compressive
sensing (BCS) was proposed. In the indoor multi-path environ-
ment, the transmission channel impulse response is estimated
accurately using the proposed approach, then we adopt the
method of direct path (DP) detection to estimate the time of
arrival (TOA) which can be used to calculate the transmission
delay, finally, the target location can be located by the weighted
least square (WLS) algorithm. From the simulation results, we
find that the proposed method compared with the traditional
localization algorithm not only the localization accuracy is
guaranteed, but also the ADC sampling rate is reduced, at the
same time, it is advantageous that compressive sensing (CS)
method applied in the UWB localization system.
Keywords-Bayesian compressive sensing; channel estimation;
time of arrival; weighted least square; ultra-wideband localization
I. I
NTRODUCTION
In recent years, due to the navigation tracking, detection,
and other areas of the demand for precise localization, making
UWB localization once again becomes a hot topic of wide
public concern, and UWB localization research continues to
grow. In impulse radio UWB (IR-UWB) localization system,
not only in theory it is available to centimeter level or even
higher localization accuracy, but also the UWB localization has
the ability of the anti-multi-path and penetrating power.
However, the high precision localization relies on the detection
of UWB signal. Therefore, a high sampling rate ADC is
required.
Because of the high cost and large power consumption of
high sampling rate ADC, difficulties in the practical
application will limit the UWB localization accuracy. CS
theory [1,2] is a new kind of sparse signal acquisition and
reconstruction technology. The multi-path component of
UWB signal is sparse, then the channel is estimated based on
traditional CS theory [3], and the reconstructed signal is
detected by the RAKE receiver. In this paper, the BCS [4]
method we used has robustness to additive noise in the
sampling process, and we need not to estimate the sparsity. In
addition, the accumulated problem of localization error is a
key issue that must be solved. To improve localization
accuracy, the WLS
algorithm is also used, which the
accumulated impact of localization error can be reduced
effectively.
II. UWB
L
OCALIZATION
B
ASED
O
N
T
HE
TOA
R
ANGING
Because UWB signals has the high time resolution, higher
localization accuracy can be obtained by the method of TOA
[5]. In the indoor multi-path environment, essentially the
estimation transmission delay is the problem of UWB signal
multi-path components detection. DP is the first arrived
multi-path components and the energy is the strongest. As
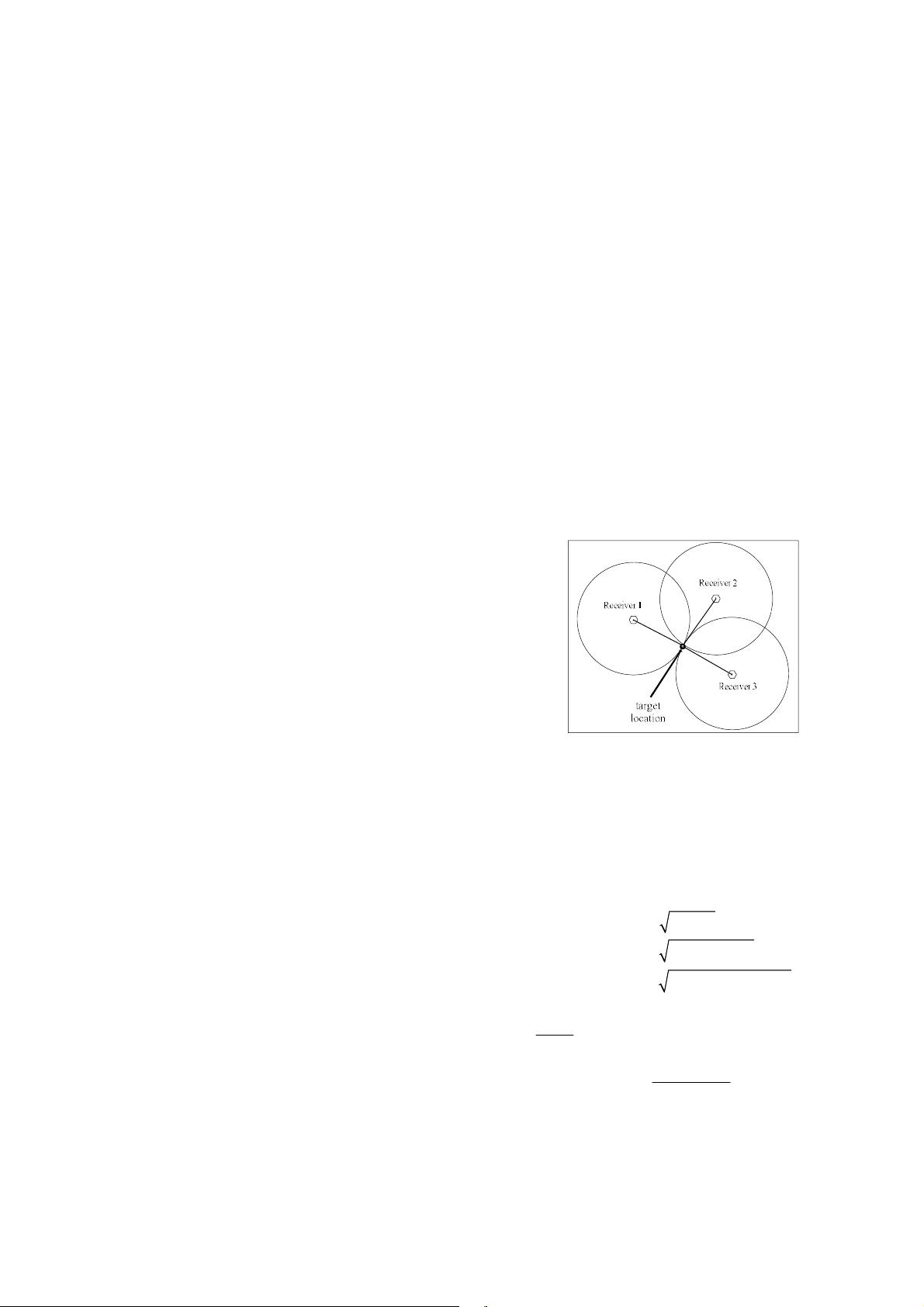
shown in figure 1, in the planar UWB localization, when the
target signal reaches more than three reference receiver, the
method of TOA estimation is detected by the arrived time of
DP. The estimation delay and the distance between the
transmitter and receiver can be known at the same time. Lastly
we take the reference receiver of a circle. Then the target
location can be measured by three circle intersection. The clock
synchronization between the transmitter and receiver, also at
least three receivers, is required in this approach.
Figure 1.
UWB localization in the planar
In the ideal case, we ignore the measurement error. Three
receivers is formed by circle intersect at one point. Without
loss of generality, we assume the receiver locations as follows:
the receiver 1: (0, 0), receiver 2: (0,
), receiver 3: (
,
).
And the target location is (
,
). Respectively the estimation
of TOA is
,
,
, then the distance between the reference
receiver and the target transmitter can be expressed as:
11
ˆ
τ
==+
(1)
22 2
ˆ
τ
==+−i (2)
33 3 3
ˆ
τ
==−+−i (3)
From (1), (2), (3), we can obtain:
2222
32
1
2
xy
= − − +−+
(4)
2
2
y
y
+−
=
(5)
___________________________________
978-1-4673-2197-6/12/$31.00 ©2012 IEEE
ICSP2012 Proceedings









