ASHRAE国际期刊：加热通风与空调研究

版权申诉

110 浏览量更新于2024-07-20 收藏 11.32MB PDF 举报

ASHRAE (美国采暖、制冷与空气调节工程师学会) 国际期刊《供热、通风与空调及制冷研究》(International Journal of Heating, Ventilation, Air-conditioning and Refrigerating Research) 是由该学会主办的一本专业学术期刊，旨在发布和探讨暖通空调领域的最新研究成果和技术进展。期刊编辑团队由Reinhard Radermacher博士领导，他担任美国马里兰大学机械工程系环境能源工程中心的主任，该中心致力于推动行业的技术创新。期刊的编委会成员包括多位国际知名学者，如James E. Braun博士，他拥有普渡大学机械工程学院的教授职位；Alberto Cavallini博士，来自意大利帕多瓦大学物理技术系的教授；Qingyan Van Chen博士，是印第安纳州普渡大学西拉斐特分校机械工程学院的教授；以及Arthur L. Dexter博士，英国牛津大学工程科学系的教授，他的专业背景涵盖了工程科学领域。Srinivas Garimella博士则在Advanced Thermal Systems Laboratory担任副教授和实验室主任，他专注于高级热系统的研究。文章版权属于ASHRAE，并受到IHS的许可分发。未经许可，不得进行复制或网络传播。许可证编号为Naval Aviation Depot/5918326100，有效期至2008年1月19日。这表明ASHRAE对期刊内容的管理和知识产权保护非常严格。《ASHRAE IJHVAC 10-4.pdf》文件可能是期刊中的一期或者一篇特定论文，它可能涵盖了暖通空调系统的设计、效率提升、可持续性、能源管理、新技术应用等相关主题。对于从事暖通空调工程、建筑环境控制、节能技术等领域的专业人士来说，这是一份重要的参考资料，能够提供最新的理论研究和实践案例，推动行业的发展和标准制定。

VOLUME

10,

NUMBER

OCTOBER

2004

Table

Frost Density Correlations

(pff

No.

Geometric

Configuration

Equation

(or

Equation Set)

Units Operational Limitations Date Reference

Range

DI FLATPLATE pf= 650 exp (0.277

qs)

kg/m3

T,=-YC

Obtained at I977 Hayashi

-18.6"C room

to 450

min

temperature

Tw=-5"Cto

Max.

1992 Maoet.al.

-15°C density

200

kp/m3

23'C

assumed

D2 FLATPLATE

15'C to

1.15

Tfi=O°C

2.67

mlr

.~.-

T,,,=-2OS0C Only for flat 1999 Mao et. al.

to4l"C

plate

D3 FLATPLATE

1.714

io-4(x*~~~056(~-o.o~'

T,=-IO.I"C

-25.8'C

3278

13112

VERTICAL p,= 0.2416(w)45°"(T)-' 827(~~~)00413(~)-5

SSI(m-0

l8i9(~~)02510

kg/m3

Tw=-lOoC Onlyforflat 2002 Leeand

PLATE to

-2OOC

plate

Ro.

5°C

2ooc

1,000

nno

-,...

kg/m3

TW=-22OC

Max.

2003 Shine1.d.

0.0479DCAo.4357 Ta= 12OC density

D5 FLATPLATE

pf=

(109.53 -45.541og(DCA))t

1.57

250

kdm'

DCA

23,

RI1

and

0.0084 m), the correlation of Mao et al. yields slightly lower frost density values. It

should be pointed out that the constraint of Mao et al.'s correlation is for

244

h and

0.0375

m), which is much lower than that in Iragorry and Tao's study. This indicates that

prolonged freezing would lead to a higher densification rate and reduce the rate of increase in

the frost surface temperature under freezer ambient conditions. In this case, in general, the lower

porosity and higher density of frost are expected, compared to the room temperature ambient

condition. From a practical point of view, the trends in Figure

under a subfreezing ambient

temperature indicate that the frost density correlates reasonably well to the frost surface temper-

ature, implying that a surface temperature sensor, such as the infrared type, might be a good

indicator for controlling a defrosting process based on the actual frost mass (through the frost

density correlation with the aid of

additional sensing signal [Iragorry and Tao

20041).

Excellent agreement was observed among the frost density correlations for the room tempera-

ture supply air in the STG range (see low frost density data in Figure

4).

After

minutes

frost growth (the start of

DBG

phase), there is a noticeable difference in the results of these cor-

relations. Much higher values are obtained with the exponential correlation of Hayashi et al.

(1977)

compared to the results obtained using the product of power functions by

Mao

et al.

(1992, 1999),

Lee and

(2002),

or Shin et al.

(2003).

In general, high values of density are

expected as the frost surface temperature approaches the water triple point, and a curve like the

one depicted by the exponential function

Hayashi is a good representation of the expected

results for convection at room temperature and is therefore recommended. It has been observed

on refìigeration evaporator coils that the

type

of frost that is characterized by frost density is

related to, among other factors,

the

temperature difference between ambient air and coil surface.

Denser frost tends to be formed on the coil surface when the temperature difference becomes

smaller. On the other hand, low-density snowlike frost would form when this temperature differ-

Provided by IHS under license with ASHRAE

Licensee=Naval Aviation Depot/5918326100

Not for Resale, 01/19/2008 02:26:33 MST

No reproduction or networking permitted without license from IHS

--`,`,`,``,,`,`,,,`,``,,,`,`,,``-`-`,,`,,`,`,,`---

402

HVAC&R

RESEARCH

700

600

500

400

300

200

100

245

250

255

260

265 270 275

Tí,

Figure 4. Frost density as a function of frost surface temperature: (a) freezer operational

conditions:

-lO°C,

-16.5OC to -28.5OC, Re

1400,

0.007

kgaíkgw;

(b)

room

air temperature

supply:

25OC,

-15OC, Re

1400,

0.007

kga/kgw,

to 120

min.

ence is large. It can be seen from Figure 4 that the trend presented by the correlations under con-

sideration is consistent with this observation.

Frost

Thickness

Table

lists empirical and semi-empirical correlations for frost thickness under different geo-

metric configurations and test conditions. The results include those presented by Mao et al.

(1 992, 1999) and Lee and

(2002), which are of the same form as the one for frost density, as

shown in Table

Semi-empirical work corresponds

the early studies by Schneider

(1978)

and Cremers and Mehra (1980), who obtained an equation for the frost thickness as a function of

the surface-to-wall temperature difference and frosting time. The methods of measuring frost

thickness range from direct measurement using mechanical means (Lee and

2002), using a

laser beam-light meter arrangement (Mao et al. 1992), to the use of video imaging (Ha0 et al.

2004; Iragorry and Tao 2004). The significance of frost thickness correlations rests in the fact

that it can be used to evaluate the evaporator coil performance and also to validate the result

from the analytical frost model.

To demonstrate the predictability of the trend in

frost

thickness, we compare the thickness

data as a function of frost surface temperature in Figure

under a room temperature test condi-

tion (Lee and

2001).

It can be seen that a significant discrepancy exists even though the same

set of conditions is applied to the correlations. This observation implies that the frost surface

temperature alone cannot be an indicator of the frost thickness.

alternative sensing mecha-

nism needs to be developed for direct detection of frost thickness. Iragony and Tao (2004) pro-

posed that an additional sensor that is capable of measuring the mass concentration, the product

frost

density,

and

thickness

would

assist

the

surface infixed sensor

detect the frost more

accurately.

Provided by IHS under license with ASHRAE

Licensee=Naval Aviation Depot/5918326100

Not for Resale, 01/19/2008 02:26:33 MST

No reproduction or networking permitted without license from IHS

--`,`,`,``,,`,`,,,`,``,,,`,`,,``-`-`,,`,,`,`,,`---

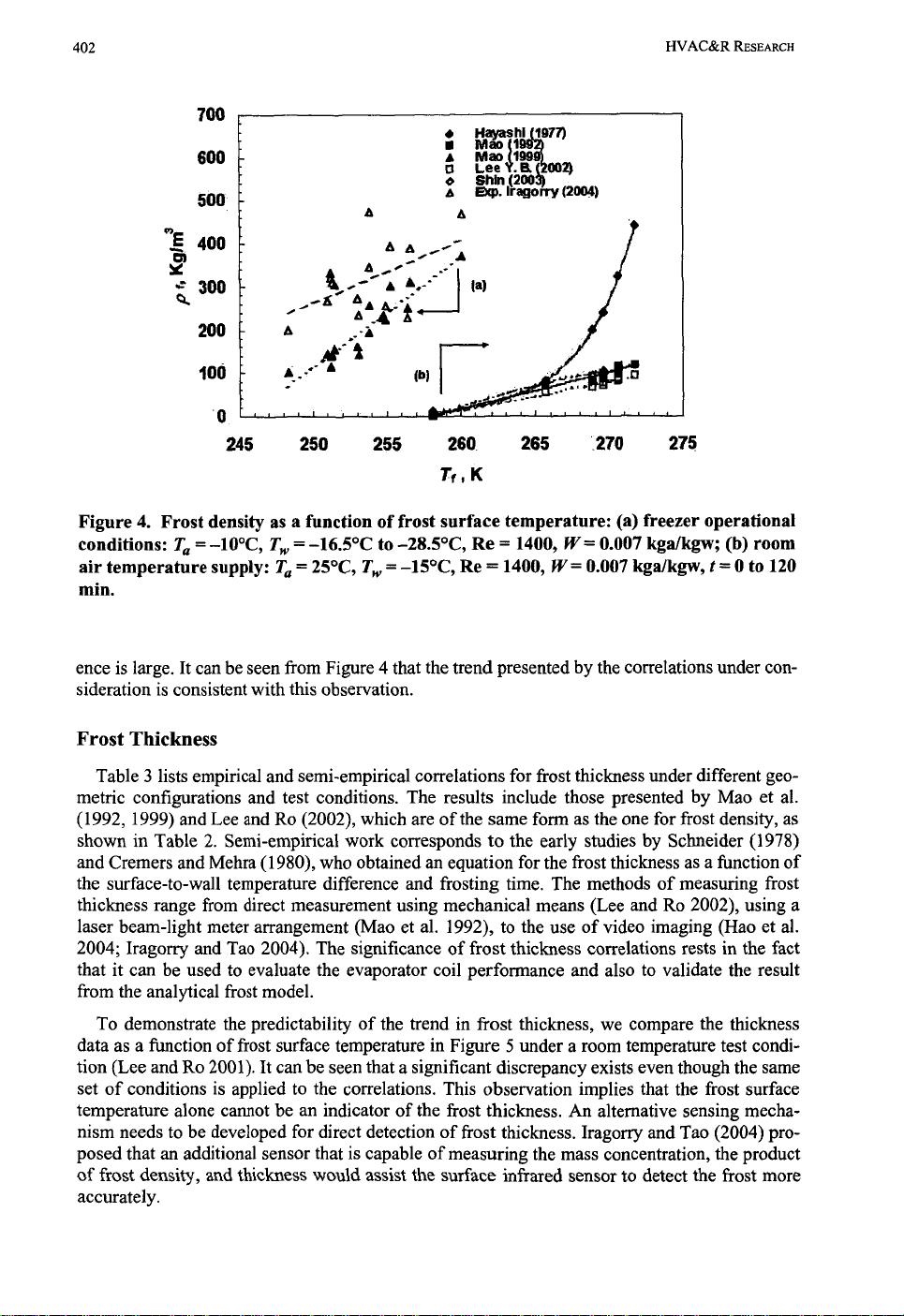
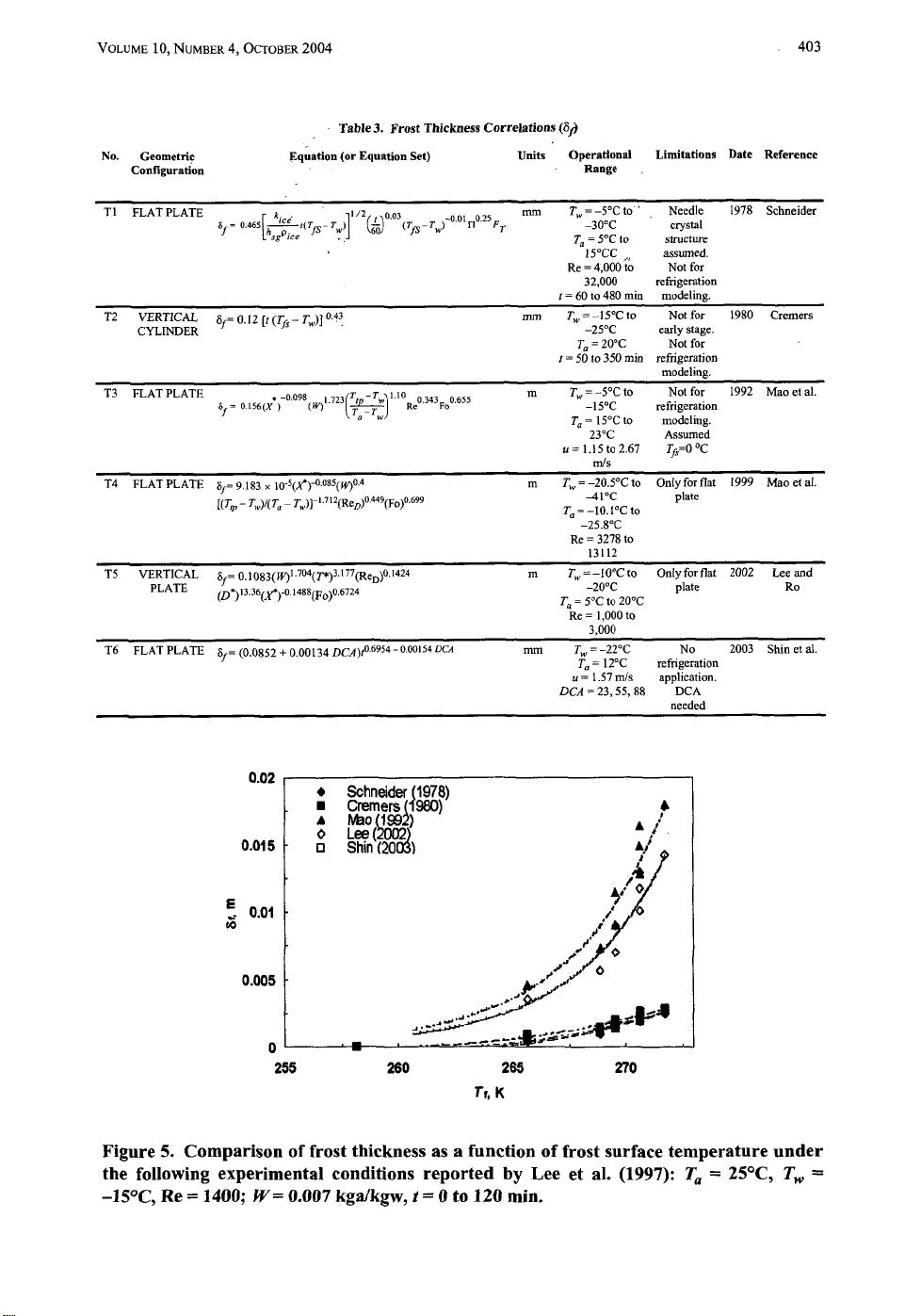
404

HVAC&R

RESEARCH

Heat Transfer Coefficient (Nusselt number)

Two types of heat transfer coefficients have been reported in the literature-one considers the

overall effect of frost on the heat transfer rate in the heat exchanger, defined with the underlying

cold surface temperature, while the other gives the heat transfer from the air to the frost layer at

the frost layer surface, defined by the frost surface temperature. Although the first definition cor-

rectly includes the latent load effect of frost on the equipment, the latter

more consistent with

the definition of reflecting convective sensible heat removed from ambient. Therefore, we only

report the latter type of correlations here, also because this is the one required in a frost growth

model. Table

summarizes the results.

can be seen, a significant number of studies have been reported in the literature. Most cor-

relations follow the same form as the classic Reynolds number or Grashof number correlations

for the nonfrosting surfaces. Two correlations by Mao et al. (1992) and O’Neal and Tree (1985)

were developed directly from their experiments where the time-dependent Nusselt number is

correlated. Although they are very useful for validating the model simulation, the use of correla-

tions has to be strictly limited to the reported range

operating conditions.

In some of the experimental work reported, the heat transfer coefficient is defined as follows:

where

is the heat flux measured from an imbedded heat flux meter on the cold surface

between the frost layer and cold plate or derived

from

the energy balance. According to the heat

balance, the above-defined heat transfer coefficient includes both the sensible heat between the

ambient and frosting surface and the latent heat due to frost growth. This explains why the

Nus-

selt number with frost

higher than that for nonfrosting surfaces, meaning the extra cooling

load for the refrigerating coil. If one needs to consider only the heat transfer between the ambi-

ent and frost surface (not the bare equipment surface), the following should hold:

PPsg

hsensible

Tydt

(4)

The second term on the right side of the above equation depends on time in a frosting process.

In many modeling studies, as will be discussed later, it

generally assumed that hsensible follows

the correlations for nonfrosting surfaces and is, therefore, independent of time if the ambient

condition remains stable. However, one may argue that under turbulent flow ambient conditions,

frost formation results in the time-dependent surface roughness that will lead to the time-depen-

dent

hsensible.

It is, therefore, necessary to conduct further studies to confirm or find the accuracy

of convective heat transfer coefficient

hsensible

under frosting conditions.

In Figure 6, a test condition is chosen to illustrate the Nusselt number calculated from various

sources. Under a given ambient and a plate surface temperature, the Reynolds number based on

the plate length is varied from

5,000

50,000.

The correlation by

Hosoda

and Uzuhashi (1967)

includes the latent heat of sublimation. The resultant

is up to three times higher than those

considering only the sensible convective heat between the frost surface and surrounding air. The

results from O’Neal

[N6

in Table 41 yield higher heat transfer coefficients, while

Yun

et al.

(2002) IN111 give lower values of

hsensible,

delaying the partition from dry surface behavior

until a Reynolds number of 3

is reached.

interesting curve results from the [N4] Gnie-

linski (1976) equation, which, at a medium Reynolds number of 2.3

lo4,

changes the projec-

tion to a more conservative value, giving the same results of

correlation.

Provided by IHS under license with ASHRAE

Licensee=Naval Aviation Depot/5918326100

Not for Resale, 01/19/2008 02:26:33 MST

No reproduction or networking permitted without license from IHS

--`,`,`,``,,`,`,,,`,``,,,`,`,,``-`-`,,`,,`,`,,`---

VOLUME

10,

NUMBER

OCTOBER

2004

405

Table

Heat Transfer Coefficient Correlations

(hc,

Nu)

No.

Geomeiric

Equation

(or

Equaüou

Set)

Units

Operational

Limitations

Dite Reference

Configuration Range

Totdl

Sensible

NI CONCENTRIC

N,,

0.018~~0.80

Re=6.8x

IO3-

innertube 1952

Kamai

ANNULUS 37 103 cooled

ReL

2.3

IO4

Steady-state 1967 Hosoda

N2 FLAT PLATE Nu

1 16ReLo.8Pp.33

11.5 x

IO4

total heat

N3 CYLINDER

W/mk Sensible 1968 Schlicbting

0.332~Re1/2Pr1/3 heat

NuD

heat

HORIZONTAL

0,73(Gr

R)’3.25

GrPr=

106to

IO7

Freeconv. 1980 Marinyuk

Sensible 1976

Gnielinski

N4 FLATPLATE

íJ/8)(ReD-

IOû0)Pr

12.7(f/8)~/~(pr*/~

CYLINDER 6 h data;

sensible

heat

N6 PARALLEL

0.034~~~0.80

6 x

IO3

50 Steady-state 1984 O’Neal

PLATE 103 sensible

heat

N7 PARALLEL

N~JN~,=

1+0.23

óuro)

time constant Transient. 1985

O’Neal

PLATE

transient time

N8 CYLINDER

Steady-state 1985 O’Neal

sensible

heat

-5°C to

Max.

1992 Maoetal.

-15°C density

N9 FLATPLATE

o,720~x*~~wo,z94

0.729R,o.72~

0.036

(Ta-rJ

FoD

15°C to 23°C 200 Kg/m3

1.15 to 2.67

Tfi

0°C

sensible

heat

N10 FLAT PLATE Nu

0.664ReI/2Pr’/’

Laminarflowover Drysurface. 1986

Holman

flat plate.

ROUGH

~,C,,U,(C~~)(O.~+(C/~)”~I~~~

W/m2K

-IOOC Turbulent 2002

Yun

et al.

25’C flow;

St,

0.8Rek0.2 P@”,

1.5 to 2.0

sensible

Cp2

(2.5

ln[84

(29.96y(t))+l])-z

(0.036

(Reo.2 0.097)

0.4 (beating) and

0.3

(cooling)

(Dittus-Boelter equation)

heat

NI2 CYLINDER NuD= 0.023ReD4’sPr

0.75Prs 160

Dry

surface 2002 Incropera

ReD

10,000

and

DeWitt

For the same freezing air conditions as for the flat plate configuration, Figure

also shows the

Nusselt number for a frost-covered cylinder using the cited correlations, compared with the val-

ues from the Dittus-Boelter equation (Incropera

1991)

that is applicable to the nonfrosting cylin-

drical surface. We may note that for this configuration, the Reynolds number varies with time

due to change in apparent cylinder diameter (with

added frost thickness). Therefore, the com-

parison with the dry-cylinder result is not appropriate unless the correction to the Reynolds

number is made by subtracting the frost thickness. Nevertheless, as shown Figure 6b, it would

set up an upper limit value among all of the correlation results. The minimum Reynolds number

for this plot is the point at which these correlations result in the same value as expected for natu-

ral convection given by Marinyuk

(1980) p5].

In general, the Nusselt number for this geometry

is expected to fall between the values given by O’Neal and Tree

(1985) (m8]

for the upper

limit) and that of Schlichting

(1968) ([N3]

for the lower limit).

ANALYTICAL AND

NUMERICAL

MODELS

During last ten years or

so,

many efforts have been made to advance the predictability

the

frosting process, especially in the area of distributed computational analysis. Due to the com-

Provided by IHS under license with ASHRAE

Licensee=Naval Aviation Depot/5918326100

Not for Resale, 01/19/2008 02:26:33 MST

No reproduction or networking permitted without license from IHS

--`,`,`,``,,`,`,,,`,``,,,`,`,,``-`-`,,`,,`,`,,`---

剩余190页未读，继续阅读

制冷技术咨询与服务

粉丝: 4044
资源: 2万+

ASHRAE国际期刊：加热通风与空调研究

ASHRAE IJHVAC 11-4: 美国采暖与制冷工程研究

ASHRAE IJHVAC 8-4: 美国采暖与制冷工程研究期刊

ASHRAE IJHVAC 14-1：HVAC&R Research期刊文章

ASHRAE IJHVAC 4-4.pdf

ASHRAE IJHVAC 2-4.pdf

ASHRAE IJHVAC 3-4.pdf

ASHRAE IJHVAC 11-4.pdf

ASHRAE IJHVAC 12-4.pdf

ASHRAE IJHVAC 7-4.pdf

ASHRAE IJHVAC 4-3.pdf

最新资源