最小树与最小树形图：网络优化中的经典问题

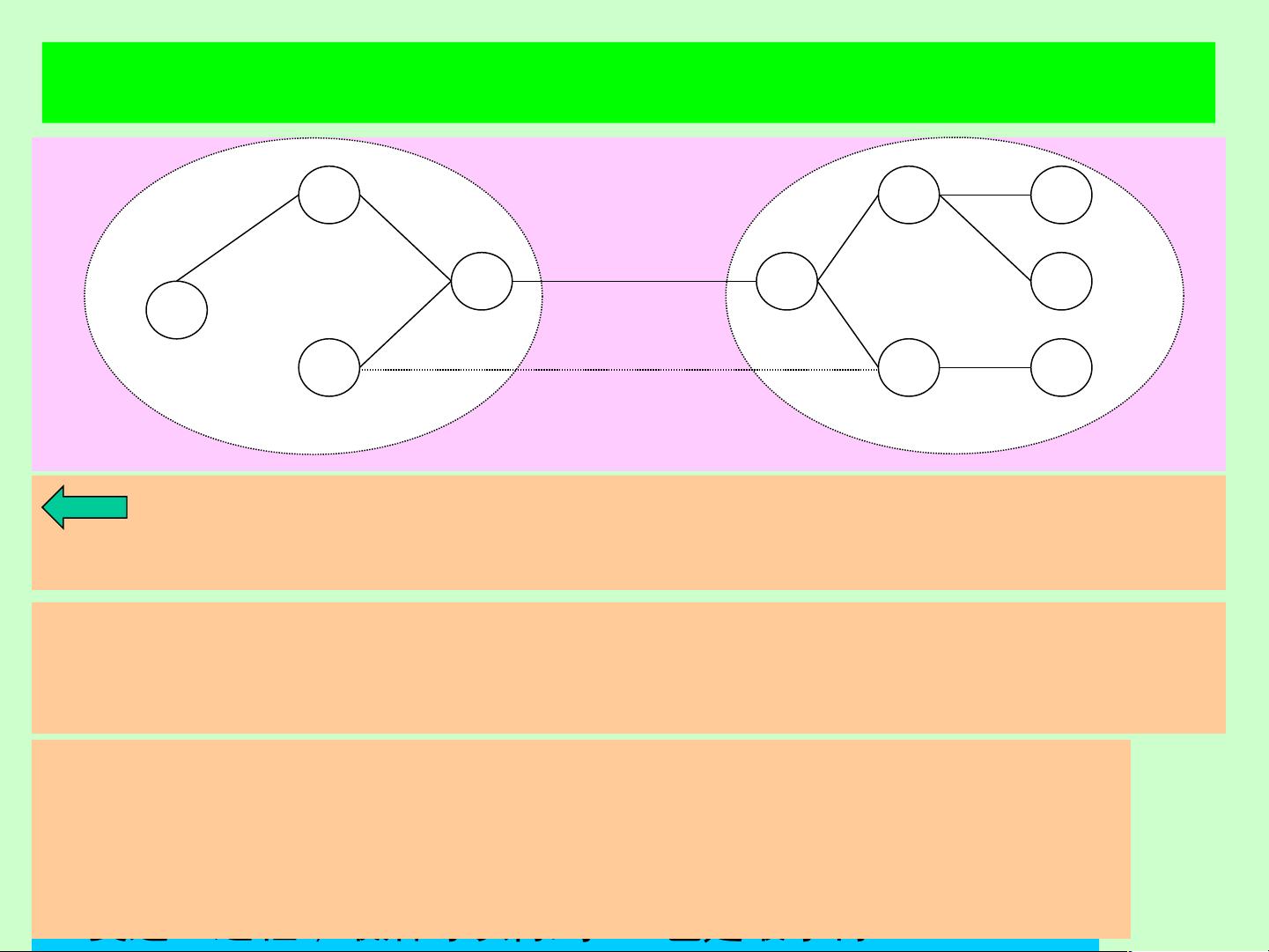
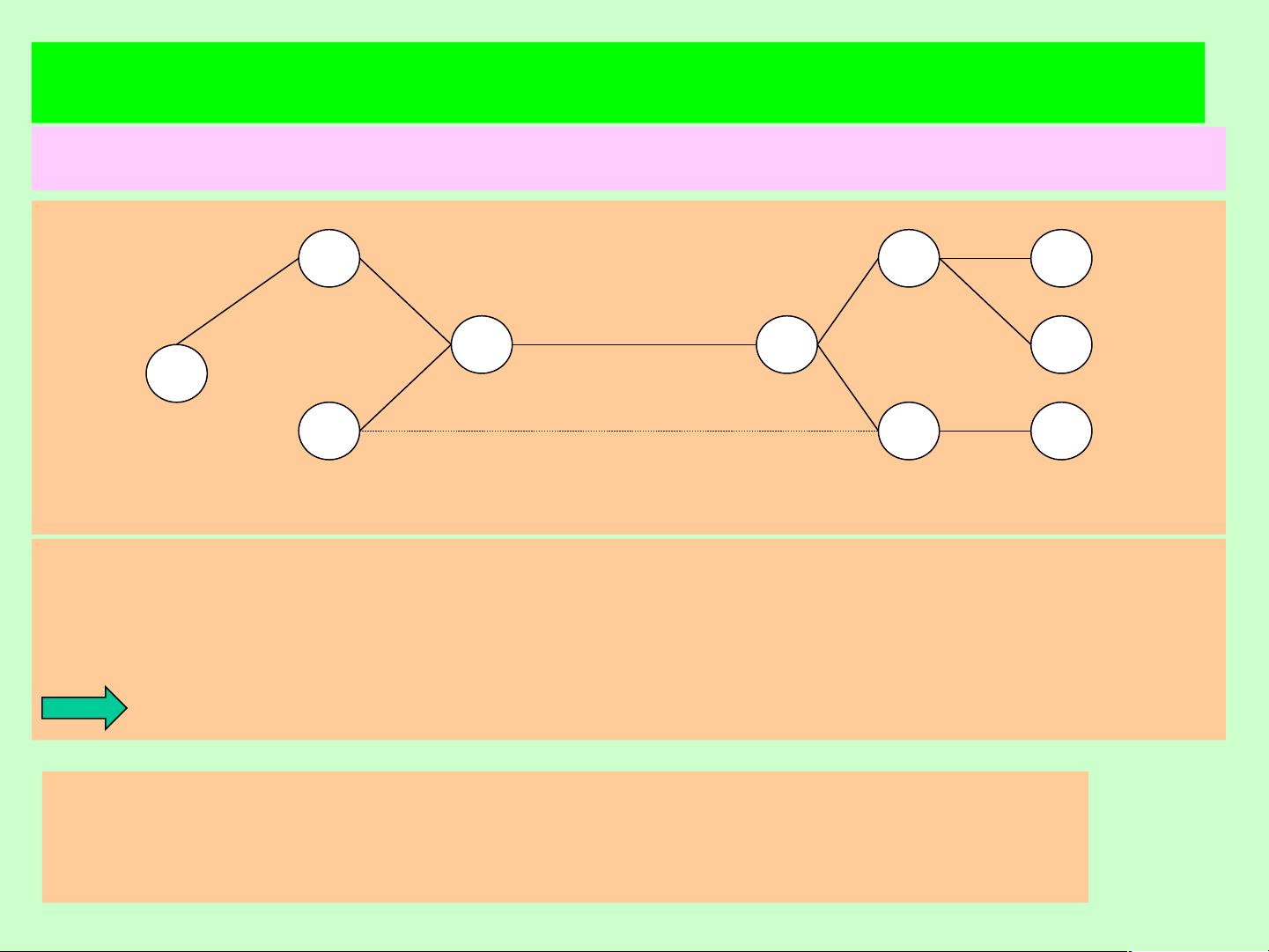
"最小树与最小树形图是网络优化中的一个重要概念，主要涉及如何构建成本最低的连通网络。这个问题通常出现在城市间的高速公路建设、电网络分析、最短路径计算等多个领域。在这个主题中，我们将探讨最小树的基本概念、等价定义以及最小树问题的应用。 最小树问题的核心是找到一个无圈且连通的支撑子图，即树，以最小化总成本。在给定的完全图G中，每对城市间都有一条边，边的权重代表了建设成本。要解决最小树问题，我们需要构建一个生成树，使得所有边的总权重最小。这样的树被称为最小树。 树的一些基本特性包括： 1. 无圈性：树是一个没有环路的连通图。 2. 连通性：树中任意两个顶点之间都存在一条路径。 3. 弧的数量：在一个包含n个顶点的树中，边的数量是n-1。 4. 唯一路径：在树中，任意两个顶点之间存在且仅存在一条路径。 5. 删除边的影响：如果从树中删除任意一条边，将导致图变得非连通。 6. 加边形成圈：在无圈的图中，添加一条连接两个非相邻顶点的边会恰好形成一个圈。 最小树的等价定义表明，一个图是树的条件可以由其连通性、边的数量以及是否存在圈等多个角度来判断。 对于带权重的网络G=(N,E,W)，定义2.2引入了最小树的概念。在这个网络中，每个边e∈E都有一个与之相关的权重w(e)。最小树，又称最小生成树（Minimum Spanning Tree, MST），是网络G的一个生成树，其边的总权重是最小的。 解决最小树问题有多种算法，如Prim算法、Kruskal算法等。这些算法分别通过不同的策略逐步选择边来构造最小树，确保在任何时候都不形成圈，并始终优先选取权重最小的边。 在实际应用中，例如在高速公路规划中，最小树可以帮助决策者确定最经济的路线布局；在电网络分析中，最小树可以用于寻找成本最低的电路连接方式。通过理解最小树和最小树形图的原理，我们可以有效地优化各种网络结构，降低成本，提高效率。 最小树与最小树形图是网络优化的关键概念，它们在多个领域都有着广泛的应用，理解和掌握这些概念有助于解决实际问题。在后续的学习中，我们将更深入地研究如何求解最小树，以及相关的算法实现。"