Matlab中自动控制系统的阶跃响应与根轨迹分析

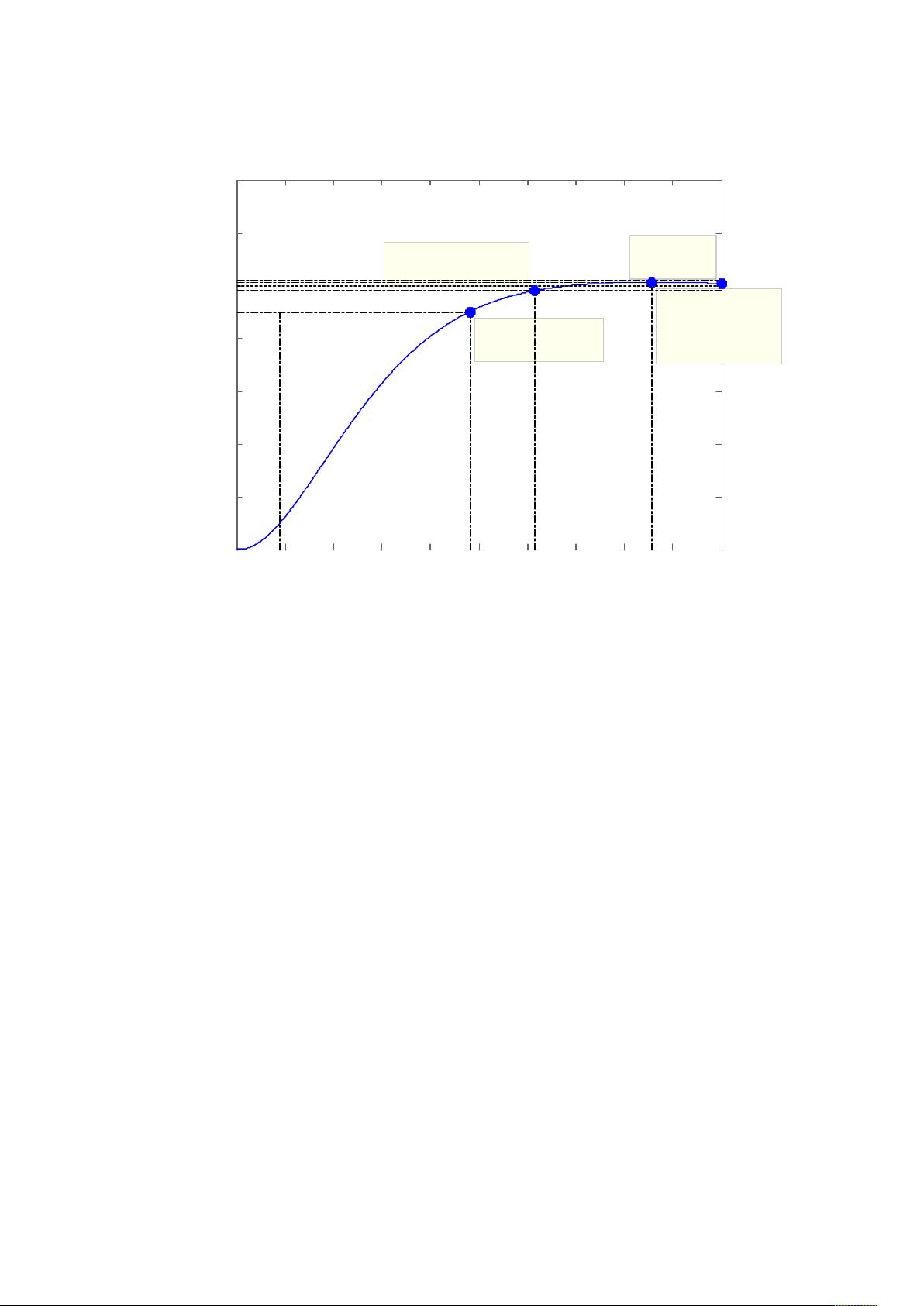
自动控制原理在Matlab中的应用深入探讨了系统设计与分析的关键技术。首先，我们聚焦于一个具有单位负反馈的控制系统，其开环传递函数为[pic]1。此部分要求我们通过`step`函数绘制闭环系统的单位阶跃响应曲线。通过观察曲线，我们可以计算出系统的主要动态性能指标，如最大超调量8.37%，上升时间和调节时间分别为1.98秒和3.59秒。值得注意的是，当阻尼比大于1时，系统响应是非周期的，最终趋向于稳态输出。 接下来，我们使用Matlab的`rlocus`函数绘制根轨迹图，展示了闭环传递函数的根在复平面上的分布。随着增益Kc的改变，比如当Kc取值为0.38、0.582、2.54和2.58时，分别观察到系统响应的变化，这有助于理解Kc如何影响系统的稳定性和性能。根轨迹图表明，系统在Kc值从0到无穷大变化过程中，稳定性呈现出明显的转变。 最后，针对Kc=5，我们进行了频域分析，通过绘制Nyquist图和Bode图来确定系统的稳定性。Nyquist图是一种评估闭环系统稳定性的重要工具，它显示了开环传递函数零点和极点在复频率域内的相对位置。Bode图则提供了幅值和相位响应随频率变化的信息，帮助我们了解系统频率响应特性。通过这些图形，我们可以判断系统是否满足奈奎斯特稳定判据，即是否存在穿越-1+j0的穿越线。 总结来说，本资源涵盖了自动控制理论中的闭环系统分析，包括阶跃响应分析、根轨迹分析和频域稳定性评估，所有这些都通过Matlab编程实现，为理解和优化实际控制系统提供了实用的工具和技术。通过实验性地调整增益参数，学习者能够深入理解系统动态行为和稳定性的关键影响因素。