6-2译码器逻辑设计与应用解析

"该教学课件是关于数字逻辑设计及应用的一个章节，专注于6-2译码器。内容包括对二进制译码器的复习，特别是3-to-8译码器（6.4.1部分）以及更大规模逻辑元素的逻辑符号（6.4.2部分）。" 在数字逻辑设计中，译码器是一种非常重要的逻辑电路。它能够将输入的二进制代码转换成特定的输出信号。在这个课件中，主要讨论了两种类型的译码器：n-to-2^n译码器，特别是2-to-4和3-to-8译码器。 6.4.1 二进制译码器（Binary Decoder） 一个n-to-2^n译码器有n个二进制输入和2^n个输出，其中只有一个输出是高电平（1），其余都是低电平（0）。这种电路被称为“1-out-of-2^n”输出编码，因为它从n位二进制输入中选择一个唯一的输出。例如，2-to-4译码器有2个输入（I1和I0）和4个输出（Y3, Y2, Y1, Y0）。每个输出Yi与输入编码的特定组合对应，如在真值表中所示。当输入使能端（EN）为高电平时，输出Yi等于输入的m_i形式，其中m_i是输入编码对应的二进制位。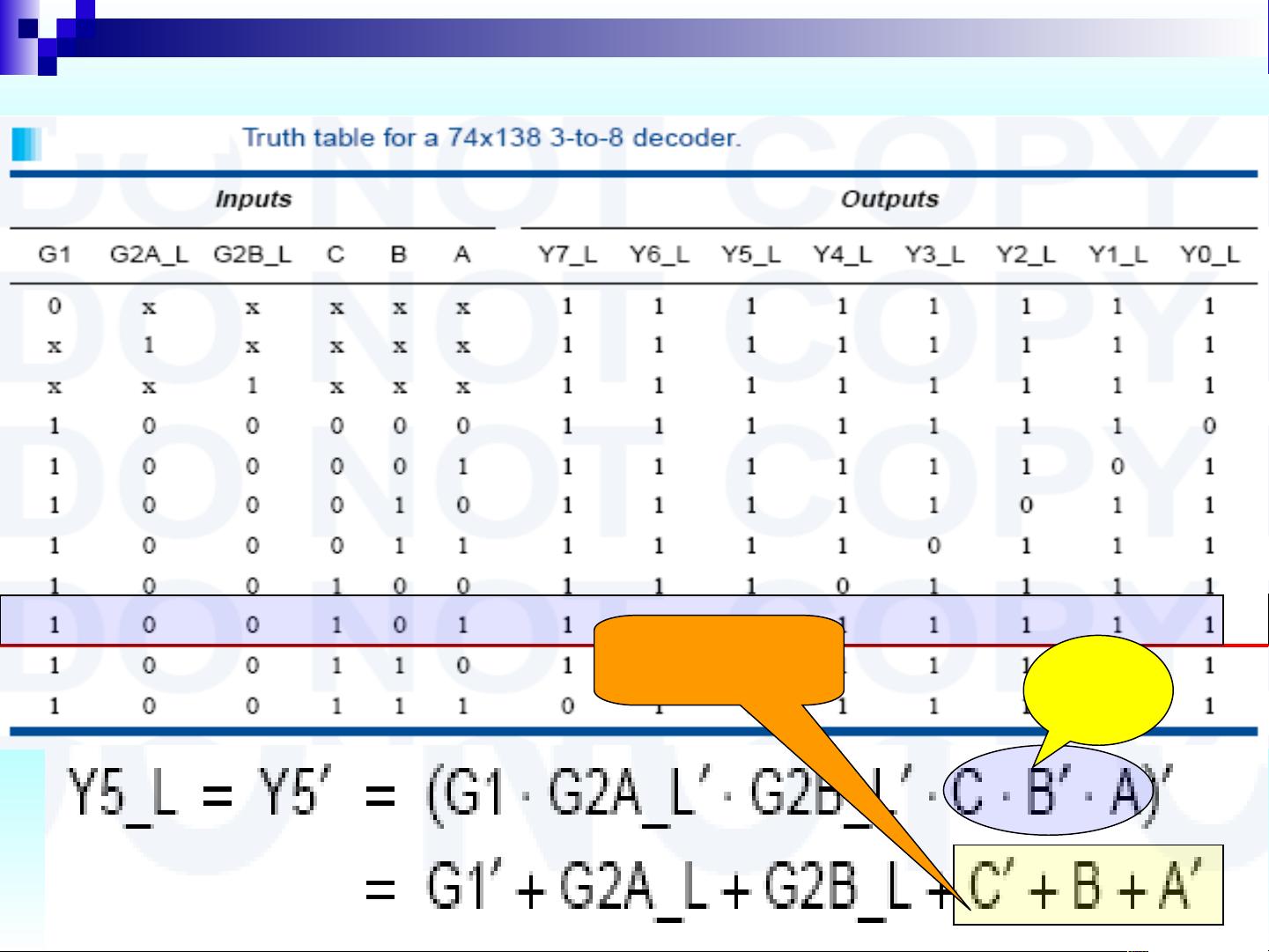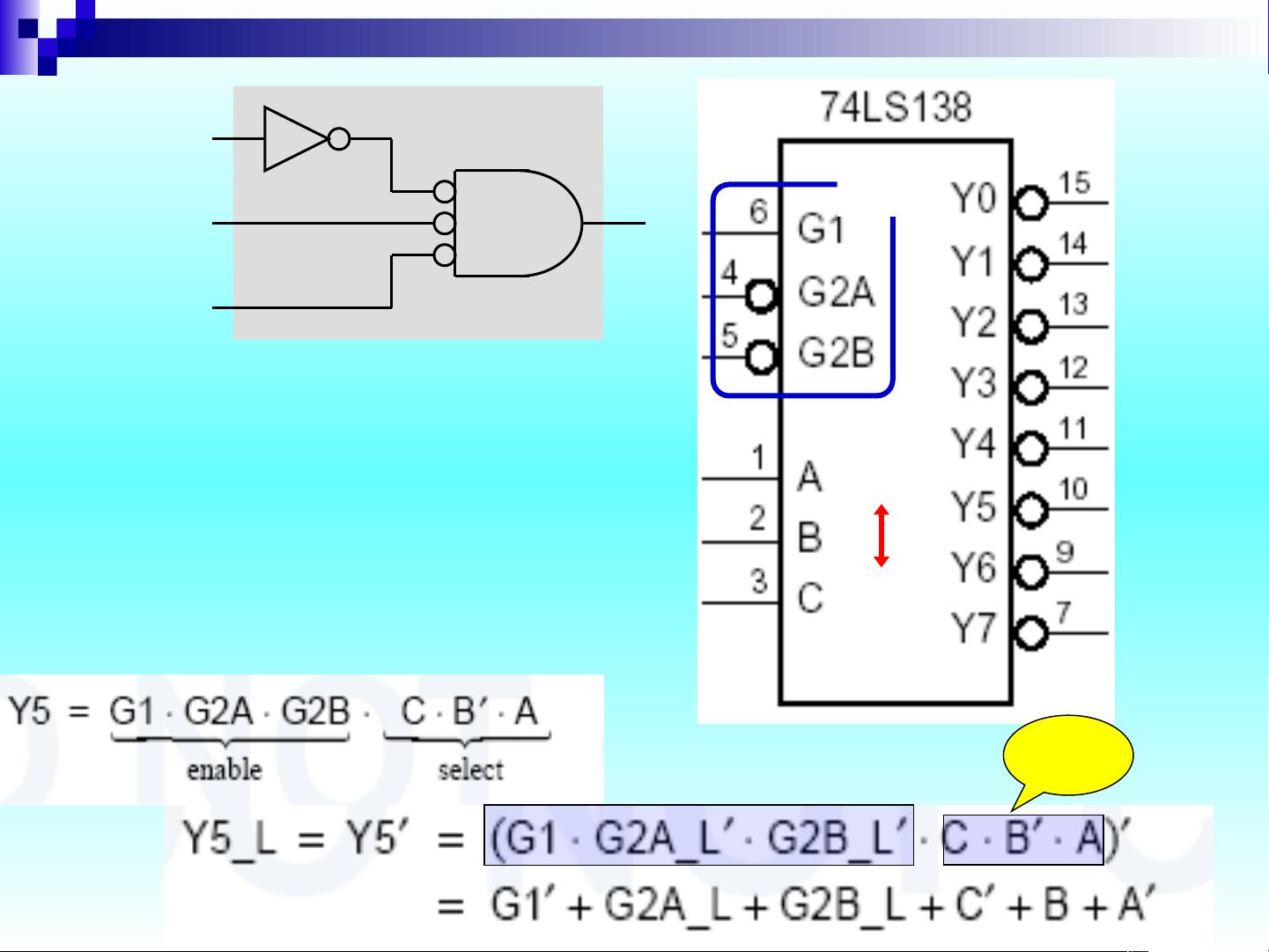 6.4.2 更大规模逻辑元素的逻辑符号 课件还提到了对于更大规模逻辑元件，如3-to-8译码器（74x138），需要使用一致的命名约定来表示内部信号。逻辑符号是描述这些元件图形化的方式，它们通常包括输入、输出和控制信号，如使能端。在设计中，使能信号（EN）通常用于控制译码器的工作状态，只有当使能端为高电平时，译码器才按照输入信号进行解码，否则所有输出均保持低电平，这被称为“无关符号”或“Don't care”状态。 实际设计练习中，如课件提到的Classexercise，学生被要求用3-to-8译码器和额外的逻辑门实现特定的逻辑函数F，例如F=AB'C + A'BC' + AB'C' + ABC'，这个练习旨在让学生理解如何通过组合使用译码器和基本逻辑门来构建复杂逻辑功能。 这个课件深入浅出地介绍了译码器的基本原理、工作方式以及在数字逻辑设计中的应用，特别关注了2-to-4和3-to-8译码器，并通过实例和设计练习强化了理论知识。对于学习数字逻辑设计的学生来说，这是一个非常实用的教学资源。