TIA博途中SCL实现快速排序详解

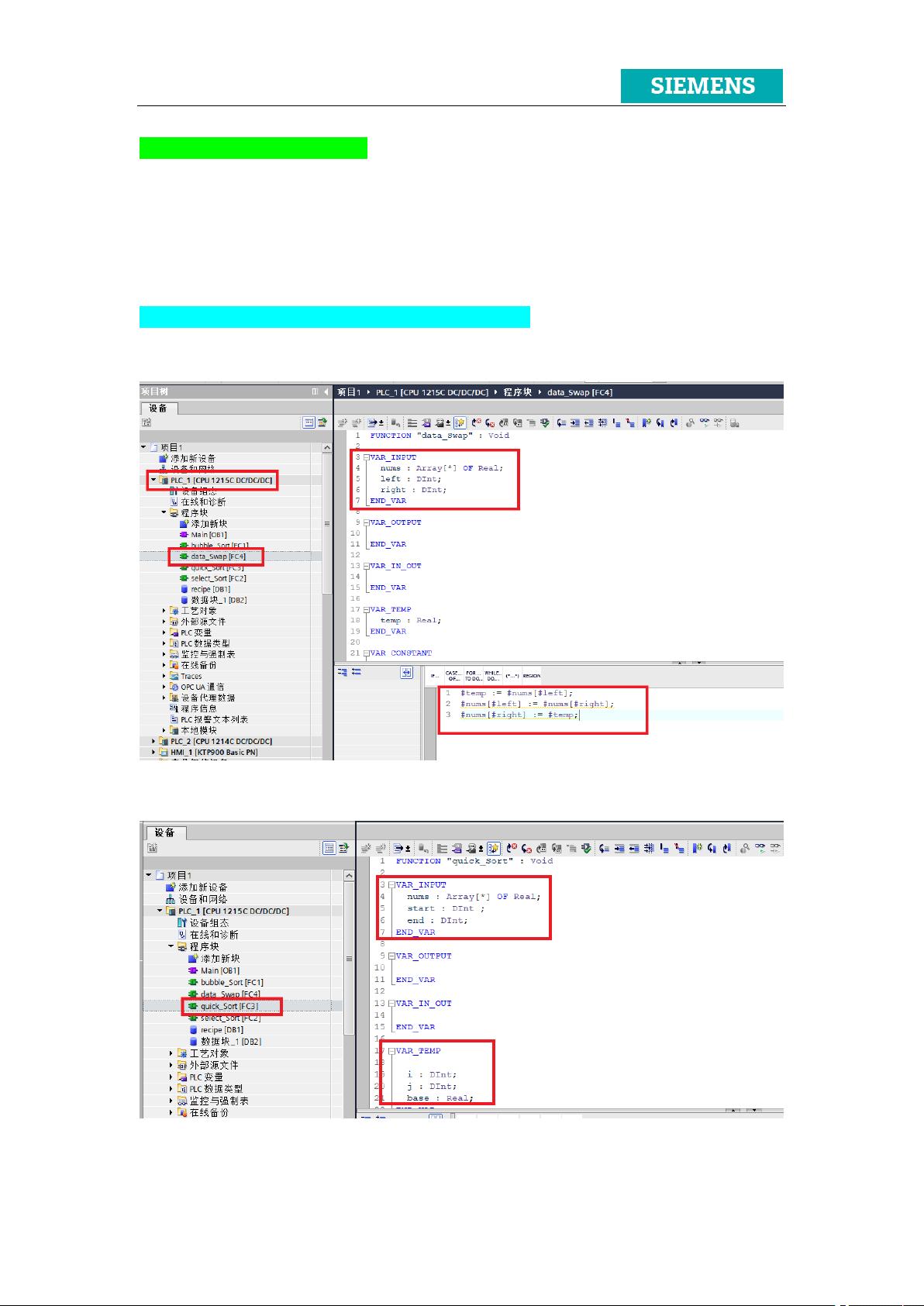
"本文档提供了一个使用TIA博途中的SCL语言实现快速排序的详细步骤，包括创建FC块、定义接口变量、编写SCL代码以及测试和展示排序效果。" 快速排序是一种高效的排序算法，源于C.A.R. Hoare在1960年提出的“Quicksort”算法。它基于分治法策略，通过选取一个基准值并重新组织数组，使得基准值左边的元素都小于基准值，右边的元素都大于基准值，然后再对左右两个子序列进行同样的操作，直到所有元素排序完成。 在TIA博途中，可以按照以下步骤实现快速排序： 1. **创建FC块**：首先，新建一个项目，然后添加两个FC（Function Block）块。一个名为"data_Swap"，用于交换数组中的两个元素，接口变量包括输入的两个元素地址和输出的新数组地址。另一个FC块命名为"quick_Sort"，负责实现快速排序算法，其接口变量包括输入数组、起始索引、结束索引以及排序后的数组地址。 2. **编写SCL代码**：在"quick_Sort" FC块中，编写SCL代码实现快速排序算法。主要逻辑包括选取基准值、分割数组、递归处理左右子序列。代码会涉及条件判断、循环、递归调用等结构。 3. **测试数据**：创建一个DB（Data Block）块，定义一个real类型的数组，并初始化为待排序的数值。 4. **调用排序函数**：在OB1（主程序）中，调用"quick_Sort" FC块，将DB块中的数组作为参数传递，并连接返回的排序后数组。 5. **结果展示**：在程序运行过程中，当触发条件（如M10.0为TRUE）时，执行快速排序，排序完成后，可以通过比较排序前后的数组，观察排序效果。 快速排序的性能特点： - **效率高**：快速排序的平均时间复杂度为O(n log n)，比冒泡排序等其他算法效率高。 - **空间复杂度**：由于采用原地排序，即在原数组上进行操作，空间复杂度较低，但递归调用会占用一定栈空间。 - **不稳定性**：快速排序不是稳定的排序算法，相同值的元素可能会在排序过程中改变相对位置。 - **最坏情况**：当输入数组已经部分或完全有序时，快速排序的时间复杂度会退化到O(n^2)。 - **分治法**：快速排序的算法思想体现了分治法，将大问题分解为小问题，逐个解决后合并结果。 尽管在最坏情况下，快速排序的时间复杂度较高，但在实际应用中，由于其良好的平均性能，快速排序通常被视为首选的排序算法之一。