"红黑树学习教案PPT：定义、特点和应用"

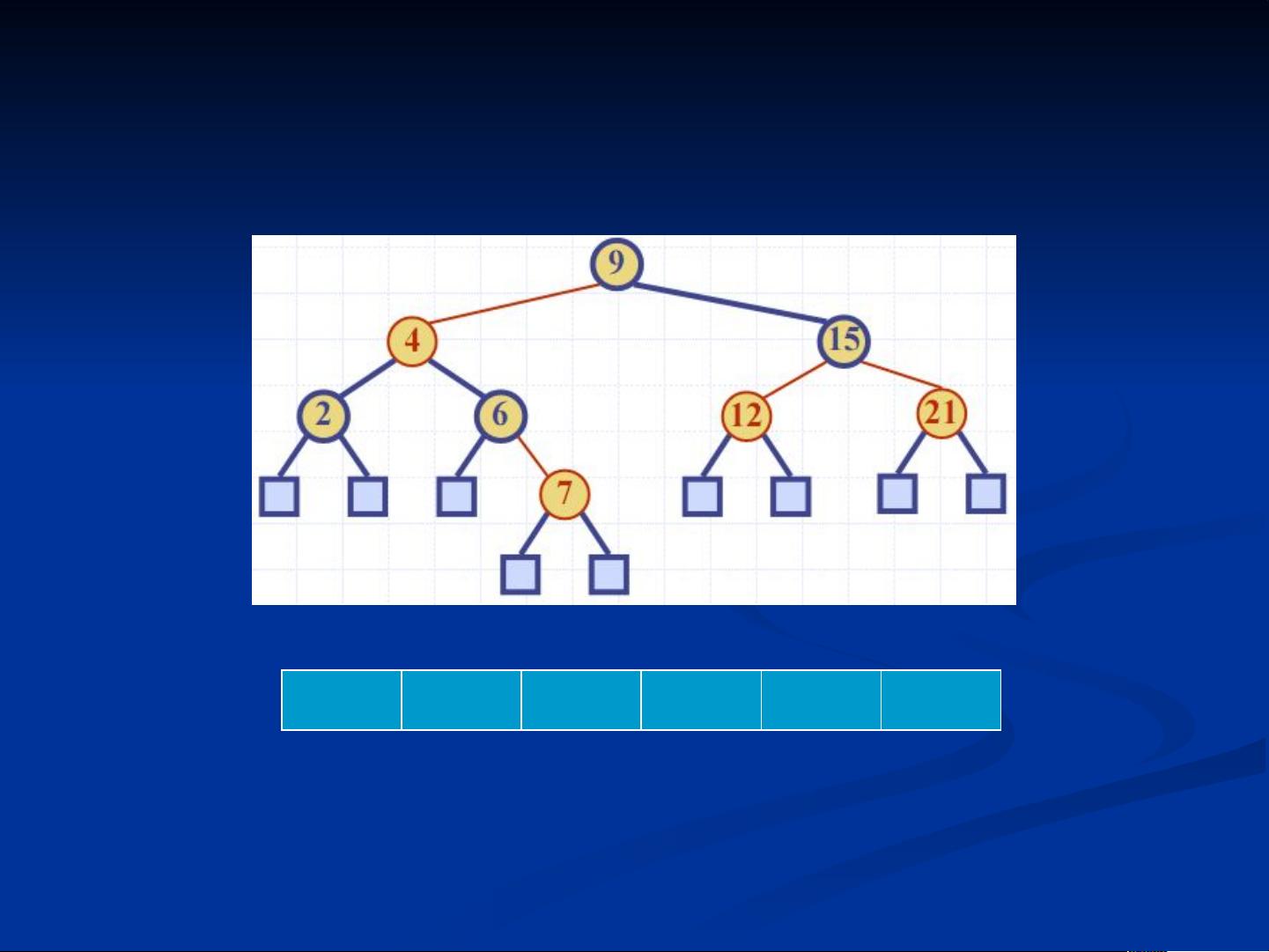
The Red-Black Tree is a type of balanced binary search tree that was invented by Rudolf Bayer in 1972 and later named by Leo J. Guibas and Robert Sedgewick in 1978. It is characterized by its use of node coloring to maintain balance, which allows for efficient operations such as searching, insertion, and deletion in O(log n) time. This makes it particularly useful for applications such as associative arrays and is utilized in various data structures such as the STL containers in C++. The Red-Black Tree is known for its ability to achieve local balance through the coloring of its nodes, which helps to reduce the strict conditions required for global balance in other types of balanced trees such as AVL trees. This allows for efficient searching, insertion, and deletion operations, making it well-suited for applications that require these functionalities. One of the typical applications of Red-Black Trees is in the implementation of associative arrays, where the keys are associated with values. It is also utilized in various data structures such as sets, multisets, maps, and multimaps. For example, in the C++ STL, the set and map containers make use of a variant of the Red-Black Tree to achieve efficient operations for storing and retrieving data. Overall, the Red-Black Tree is a versatile data structure that offers efficient operations for searching, insertion, and deletion, making it suitable for a wide range of applications in computer science and software development. Its balanced nature and efficient time complexities make it a popular choice for implementing data structures and algorithms that require these functionalities. Whether it's for maintaining associative arrays, implementing containers in programming languages, or other applications, the Red-Black Tree's properties make it a valuable tool for software developers and computer scientists alike.