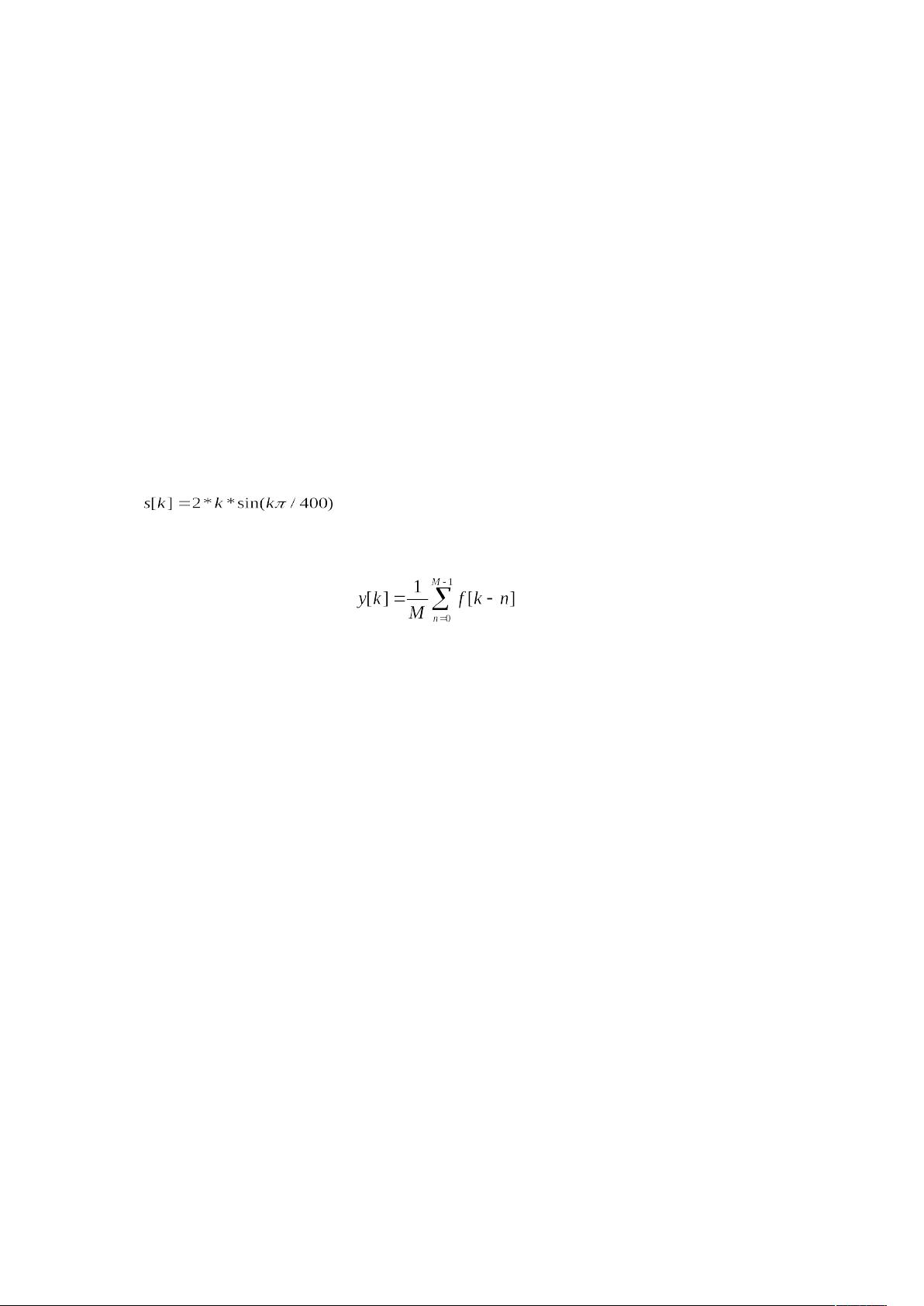MATLAB实现滑动平均滤波器去噪处理

"该资源是一份关于滑动平均系统在信号去噪中的应用的实验报告。通过MATLAB编程实现M=5和M=2的滑动平均滤波器，对比去噪效果。" 滑动平均系统是一种常见的数字信号处理技术，主要用于消除随机噪声并平滑信号。在本实验中，滑动平均系统被用来处理受到噪声干扰的信号f[k]，该信号由原始信号s[k]和噪声信号d[k]组成。噪声d[k]是通过生成在-0.5到0.5之间均匀分布的随机数来模拟的。 滑动平均系统的基本原理是通过对连续的数据点取平均来降低数据的波动性，从而减少噪声的影响。其数学表示为一个线性滤波器，输入输出关系为y[k] = (1/M) * Σ(f[i]), 其中i=k-M+1 to k，M为滑动窗口的大小，即平均点的数量。在这个实验中，M=5表示取最近5个样本值进行平均。 实验步骤包括： 1. 生成噪声信号d[k]，并结合原始信号s[k]得到加噪信号f[k]。 2. 应用M=5的滑动平均滤波器于f[k]，得到去噪后的信号y[k]，并将结果绘制成时域图。 3. 分别讨论M=2时的去噪效果。 从实验结果来看，当M=5时，去噪效果显著，大部分噪声被有效地滤除，但同时导致有用信号s[k]的部分细节丢失，使得曲线变得平滑。而在M=2的情况下，虽然去噪效果较弱，能保留更多原始信号的特性，但噪声仍较为明显。 分析图（a）、（b）和（c）可知，随着滑动平均窗口M的增大，噪声的抑制效果增强，但信号的失真也更严重。因此，在实际应用中，选择合适的M值是一个权衡过程，需要根据具体需求平衡噪声抑制与信号保真度之间的关系。 滑动平均系统提供了一种实用的信号去噪方法，适用于实时处理和对快速变化响应不敏感的场景。在MATLAB中，使用`filter`函数可以方便地实现这一过程，通过调整滤波器系数和窗口大小，可以定制化去噪策略以适应不同的信号条件。