探索三次样条插值：概念、方法与误差分析

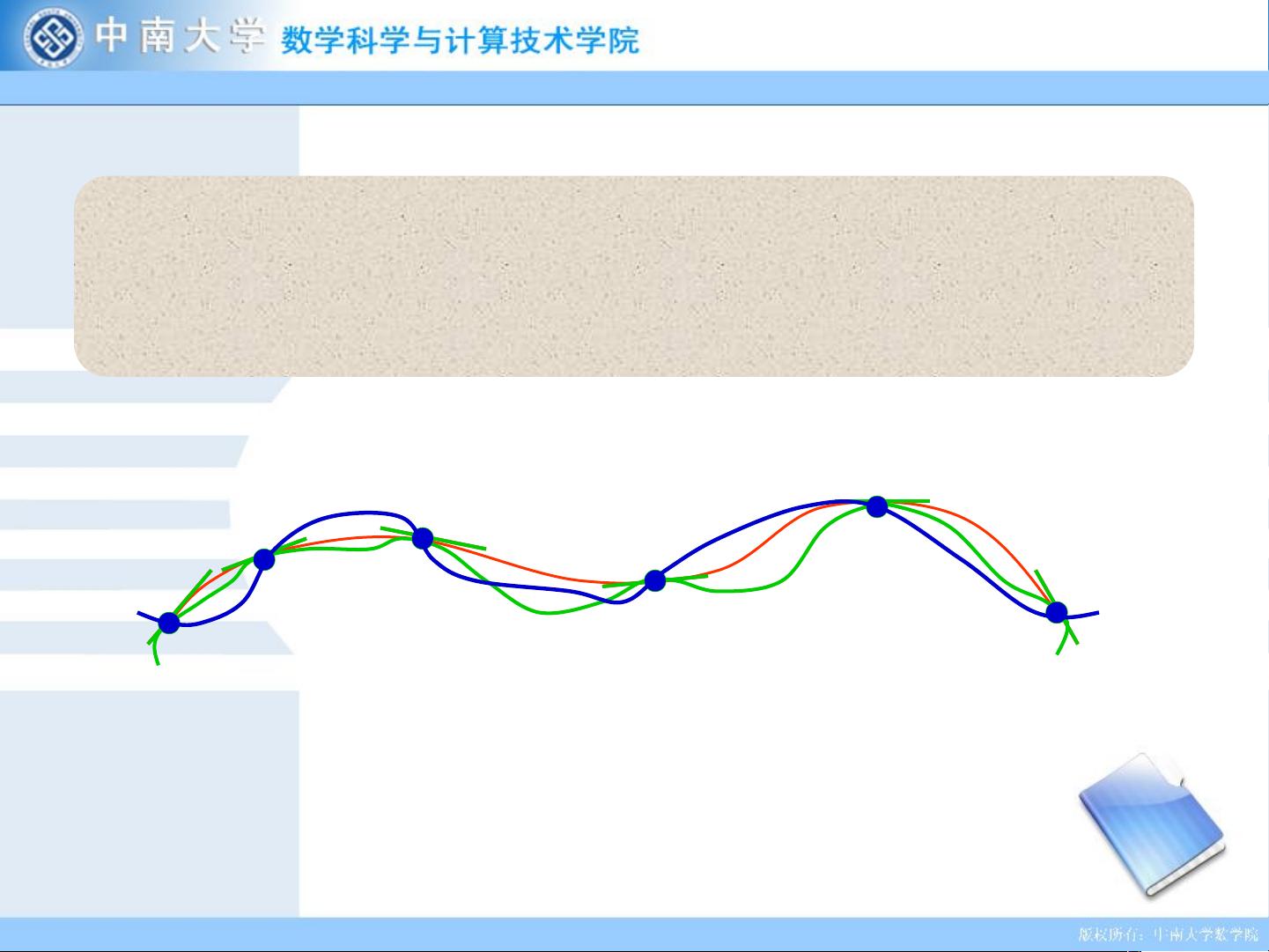
**三次样条插值** **章节概述** 本章主要探讨的是三次样条插值，这是一种高级的插值方法，用于构建光滑的曲线来近似给定数据点。三次样条插值通过定义一系列特定的函数形式，即样条函数，来克服高次插值可能出现的龙格现象（oscillations），提供更好的曲线连续性和光滑性。它源于工程领域的实际应用，例如在船舶、汽车和飞机设计中的外形拟合。 **概念介绍** 1. **三次样条插值函数的概念** - 样条插值是一种基于控制点和样条函数的插值技术，通过将细长的样条线连接在样点上，形成连续且可微的曲线，确保了函数的平滑过渡。 2. **插值步骤** - 以被插值函数 \( y = \frac{1}{1 + x^2} \) 为例，展示了如何使用 `spline` 函数在 MATLAB 中实现三次样条插值。首先，计算原始数据点（\( x \), \( y \) 对），然后定义插值点 \( \xi \)，并使用 `spline` 函数得到拟合曲线。 3. **误差估计** - 三次样条插值通常提供了误差分析的能力，帮助评估插值函数与原数据点之间的差异。对于插值函数 \( y_i \) 在插值点 \( xi \)，误差可以通过特定公式来估算。 4. **样条曲线的特性** - 样条曲线具有更高的光滑度，比分段线性插值更易控制。此外，它的导数值也更容易提取，这对于求解函数的切线和曲线的形状分析至关重要。 5. **应用实例** - 提供了一个具体的应用示例，展示了如何使用三次样条插值对一组离散数据点进行拟合，比如 \( x = [0, 0.0155, ..., 2.0] \) 和对应的 \( y \) 值，然后生成连续的曲线图。 **与其他插值方法的比较** - 与二次插值相比，三次样条插值能提供更高的精度和光滑度； - 分段埃尔米特插值虽然可以提供光滑性，但在节点处导数处理相对复杂； - 牛顿插值（L-插值）和 Hermite 插值也有局限性，特别是当数据点过多时可能出现龙格现象； - 三次样条插值通过其设计兼顾了平滑性和易用性，因此在实际工程和科学计算中更受欢迎。 通过学习本章内容，读者能够理解三次样条插值的基本概念，掌握其实现方法，并能运用到数据分析和图形拟合的实际问题中，提高数据的准确表示和可视化效果。